Space-charge-modifed eigenvectors for improved eigenpainting?
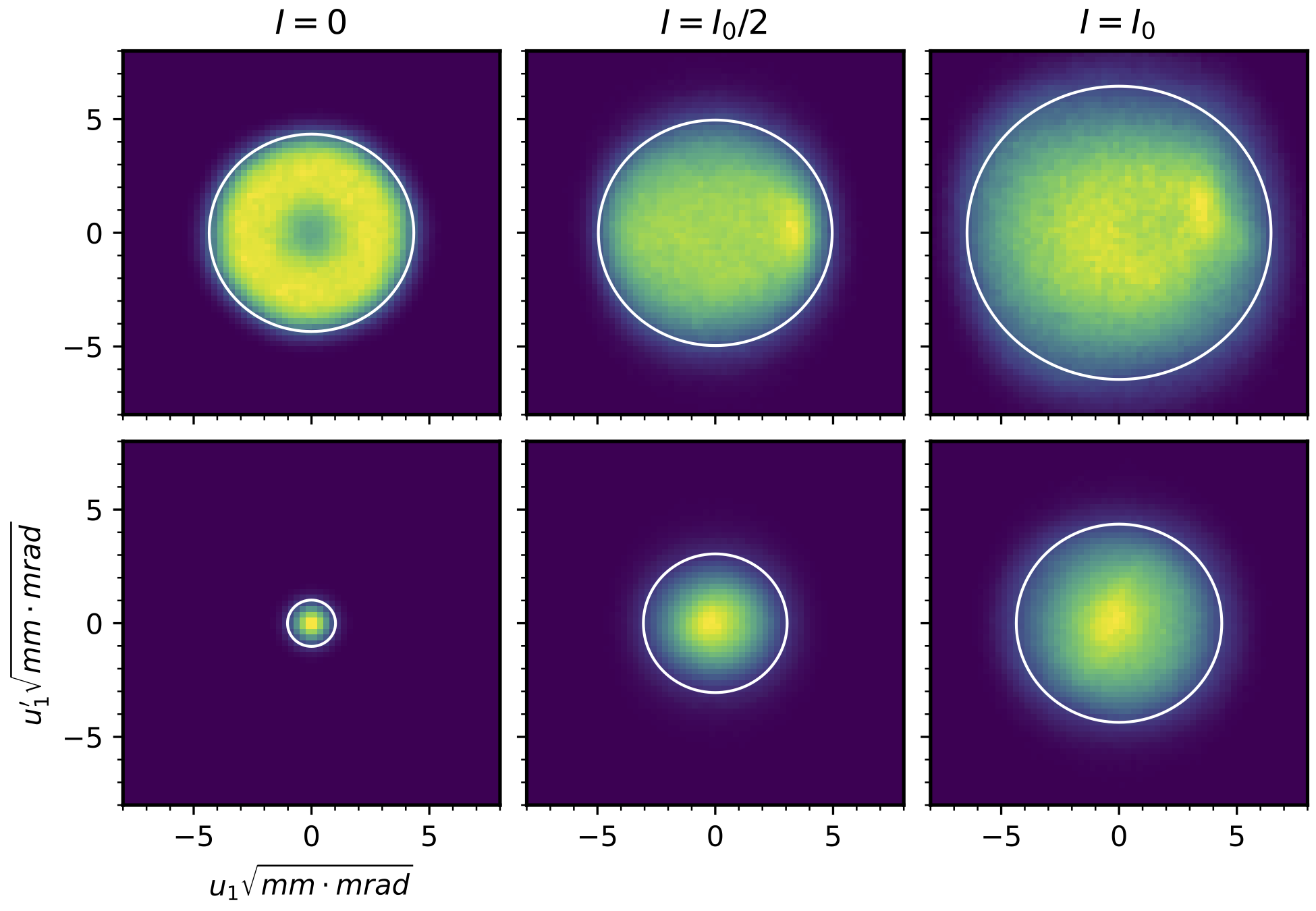
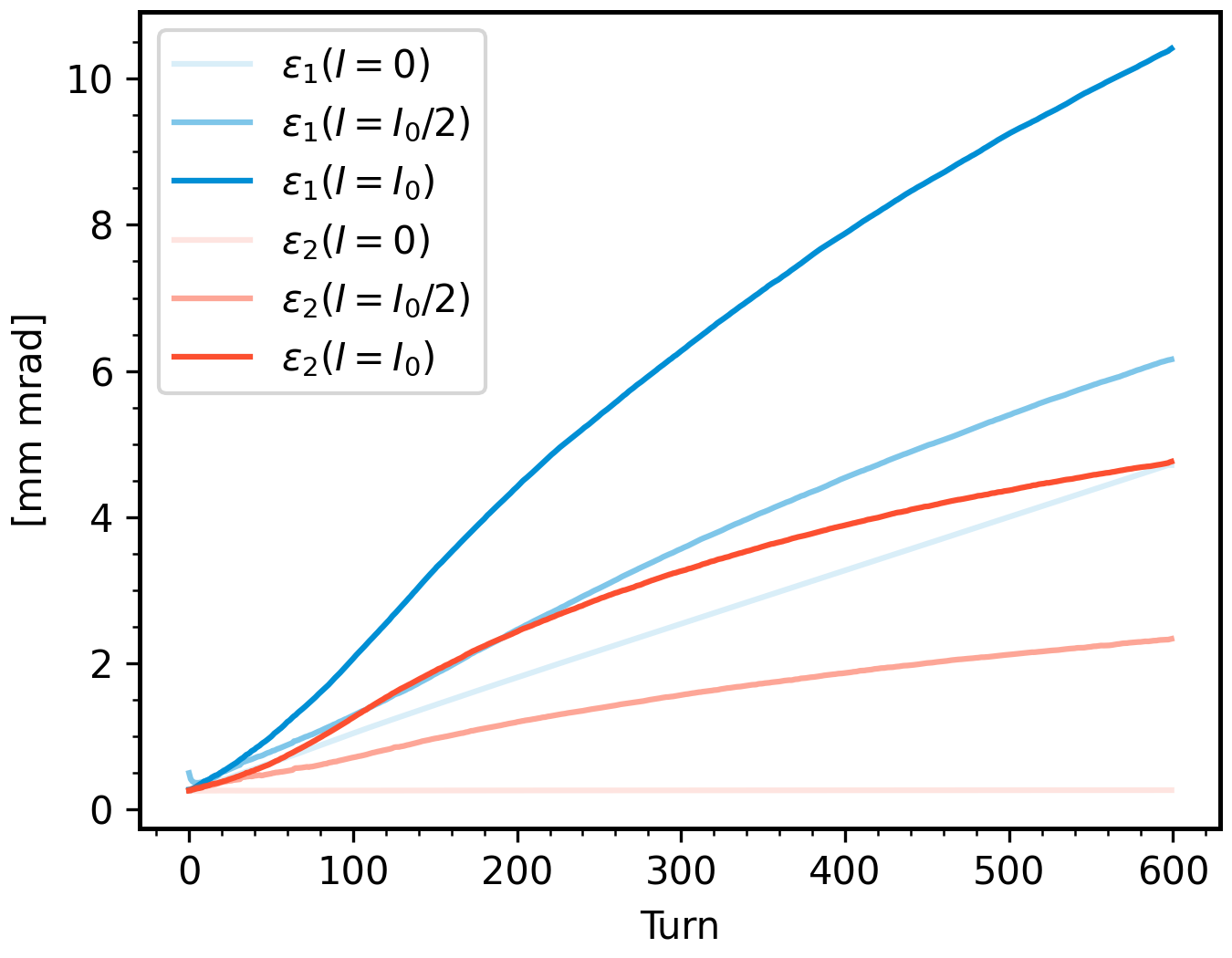
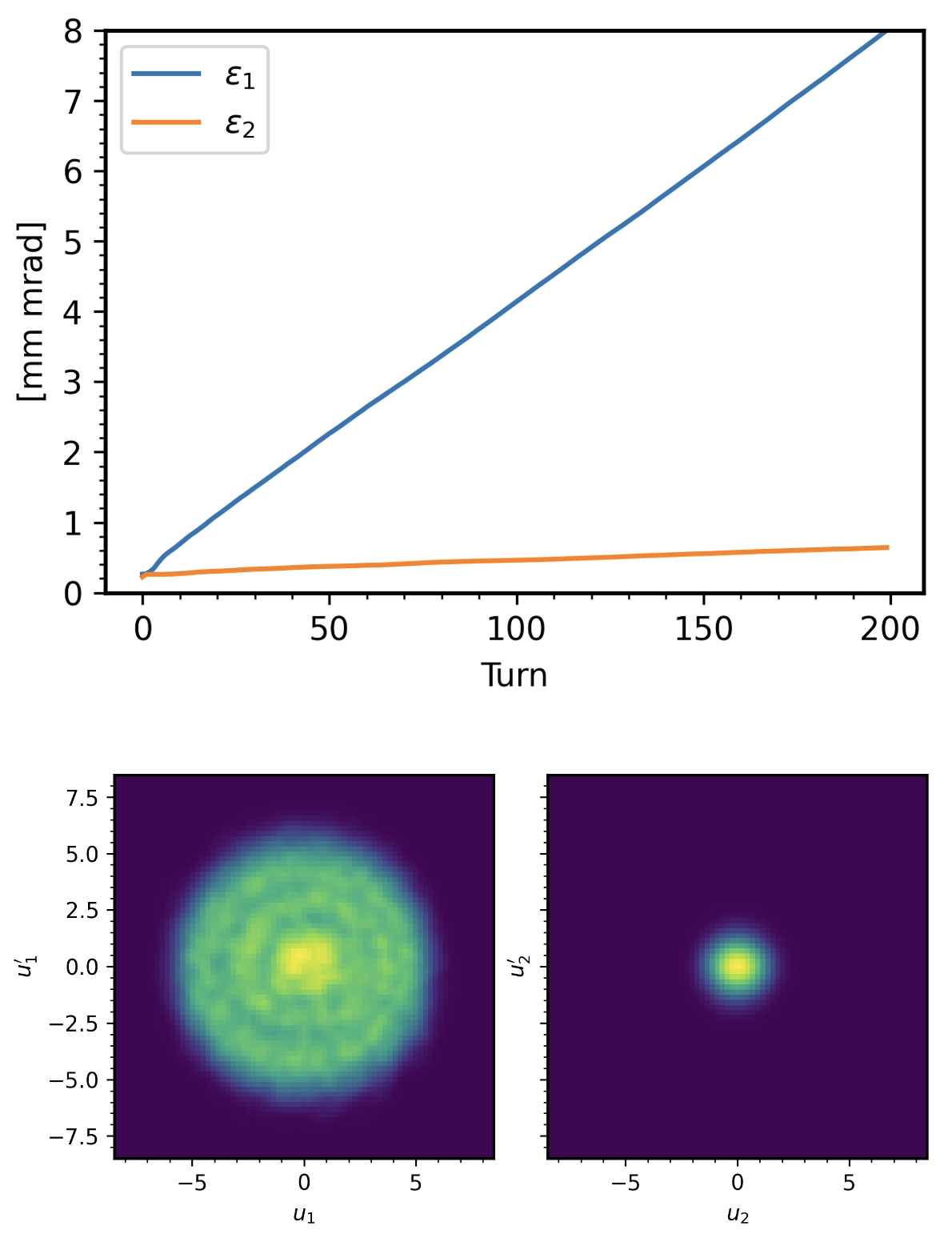
In our eigenpainting experiment at the SNS, we measured final intrinsic emittance \(\varepsilon_1 = 12.4\) and \(\varepsilon_2 = 5.1\) (mm mrad), giving a ratio \(\varepsilon_1 / \varepsilon_2 = 2.4\). The beam intensity was \(I = I_0 = 600\) minipulses, with each minipulse containing around \(1.5 \times 10^{14}\) protons within an emittance \(\varepsilon_1 = \varepsilon_2 \approx 0.25\) [mm mrad]. Here are the simulated beam distributions and emittances as the intensity increases:
The simulation without space charge predicts \(\varepsilon_1 = 4.2\) and \(\varepsilon_2 = 0.25\), or a ratio of 16. This means there was a large growth of the four-dimensional emittance \(\varepsilon_{4D} = \varepsilon_1 \varepsilon_2\) in our experiment.
I mentioned that we didn’t consider the effect of space charge on the eigenvectors. The linear component of the space charge force modifies the transfer matrix \(\mathbf{M}\) to an effective transfer matrix \(\hat{\mathbf{M}}\). Tracking a particle through the linear lattice + linear space charge kicks is the same as just applying \(\hat{\mathbf{M}}\) to the initial coordinates. For a special set of initial beam parameters, \(\hat{\mathbf{M}}\) represents a periodic focusing system. This occurs when \(\mathbf{\Sigma} = \hat{\mathbf{M}} \mathbf{\Sigma} \hat{\mathbf{M}}^T\), where \(\mathbf{\Sigma}\) is the beam covariance matrix. We want to paint along an eigenvector of \(\hat{\mathbf{M}}\), not \(\mathbf{M}\).
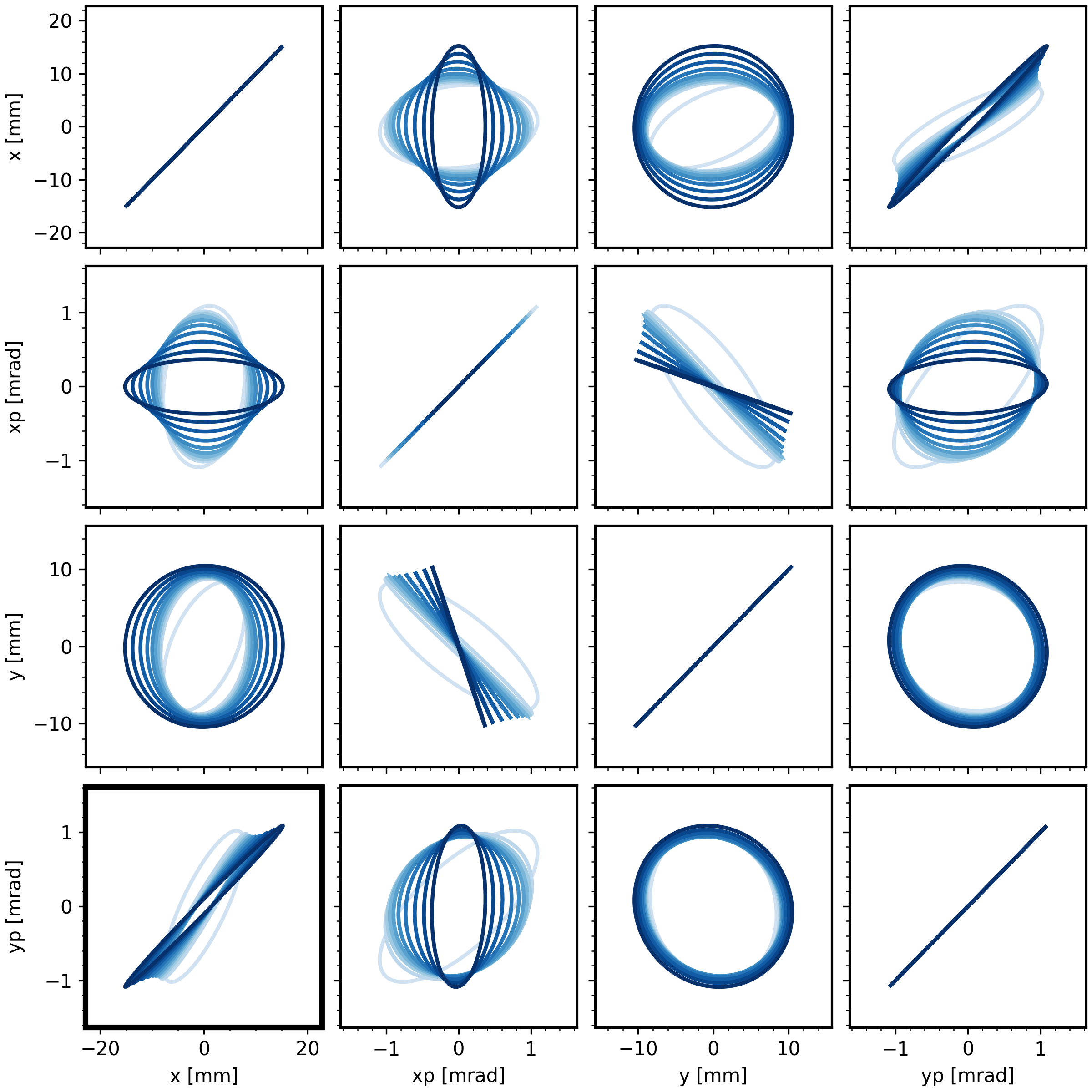
Figure 3 plots the two-dimensional projections of the matched covariance matrix (“envelope”) as the beam intensity ramps from 0 to 200 minipulses. I had trouble finding a matched solution beyond 200 minipulses, which may indicate an envelope instability. The depressed tune crosses the integer already at 100 minipulses.
Each solution is calculated with a fixed intrinsic emittances \(\varepsilon_1 = 4.24\) and \(\varepsilon_2 = 0\). It’s interesting that the \(y\)-\(y'\) distribution doesn’t change much with intensity. That’s good news for us because our main limitation is the angular coordinate, which is limited to \(y' \approx 1\) mrad. It looks like we could paint this matched solution.
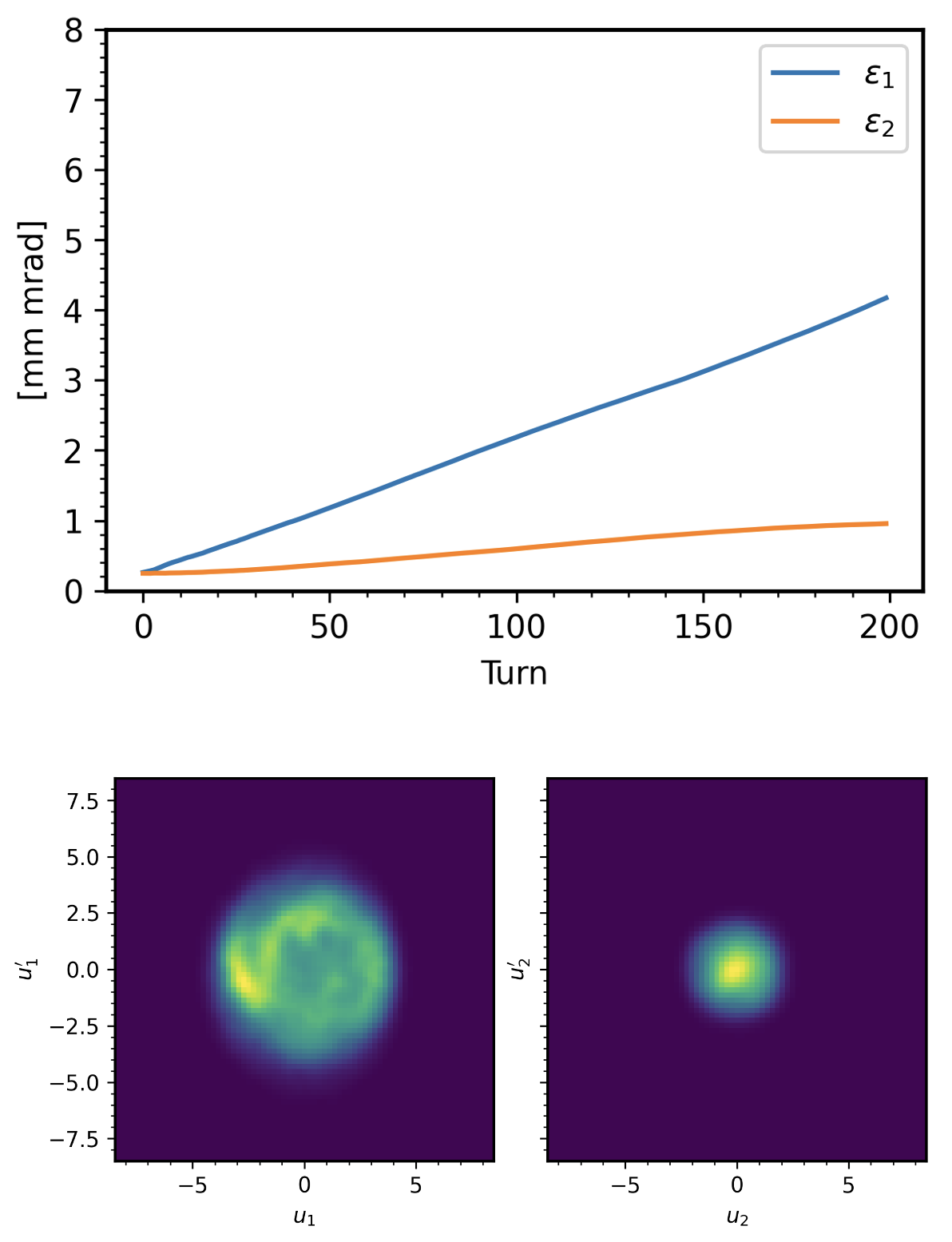
It’s not really necessary to calculate the modified eigenvectors, since Figure 3 shows that the painting path is a line in the \(x\)-\(y'\) plane. I ran a quick simulation, painting along the line \(\mathbf{x} = (20, 0, 0, 1.1)\) and using a 2D PIC model for the transverse space charge kicks. Results are in Figure 4.
The final emittance ratio is \(\varepsilon_1 / \varepsilon_2 \approx 4\) using the lattice eigenvector and \(\varepsilon_1 / \varepsilon_2 \approx 12\) using the modified eigenvector. Figure 4 (b) shows a beautiful, nearly uniform density in the first mode. I’ll need to rerun these simulations with a more realistic space charge solver and other effects included for a better estimate, but these are great results!
Luo et al. recently “demonstrated a large transverse emittance ratio of 11∶1 with gold ion beams at a particle energy of 100 GeV per nucleon, thanks to stochastic cooling and fine decoupling” at RHIC. (The cooling takes hours.) Burov writes,
To have a high ratio of the emittances, the beam has to be injected predominantly into one of the circular modes, keeping another emittance as small as possible. This could be done by means of multiturn painting with a small-emittance beam from a linac: the emittance ratio is determined then by a number of injection turns. Most likely, emittance ratio >10 would require the space charge to be taken into account at injection: otherwise a space charge related mismatch would heat the smaller emittance preventing having it that small. For a not so high emittance ratio, like 10 or so, this mismatch, probably can be ether neglected or compensated on average only. To inject into a truly space charge self-consistent state [8], allowing emittance ratio 20 or higher, the inductive synchrotron can be used [9].
If a ratio of 10 is possible in the near future, there’s good reason to think we could reach 20 or higher with stronger kickers. The emittance ratio increases linearly with time, or equivalently with the maximum injection amplitude. So if we could just increase the \(y'\) limit from 1 mrad to 2 mrad, we would double the emittance ratio. For some perspective, the projected emittances in these simulations are around 5 mm mrad, but the nominal emittance during SNS operations is like 25 mm mrad, so we’re nowhere near the beam size limit.
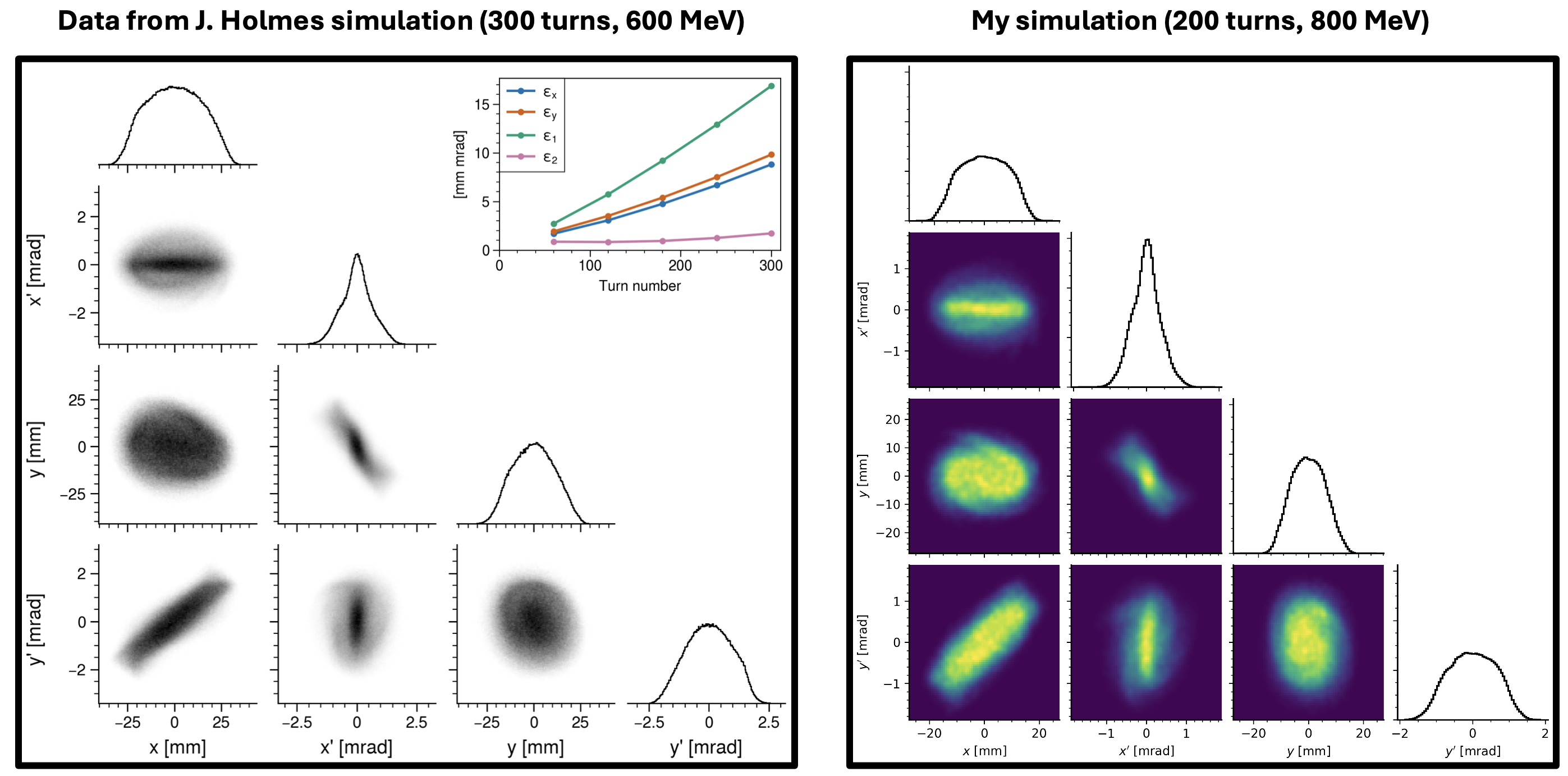
I also compared my simulation to the simulation reported here, which used a lower beam energy, different intensity, and larger painting amplitude. Figure 5 looks pretty close to me. It looks like Jeff happened to land near the modified eigenvector without trying to.