Phase space spirals

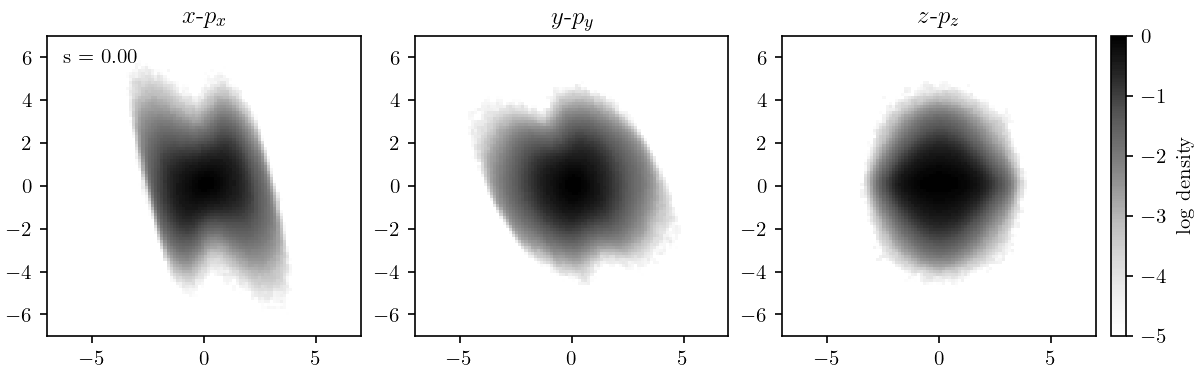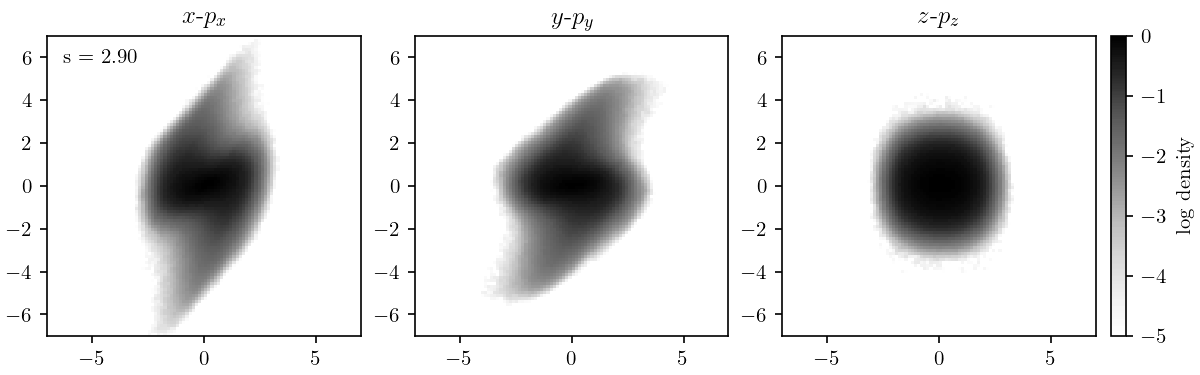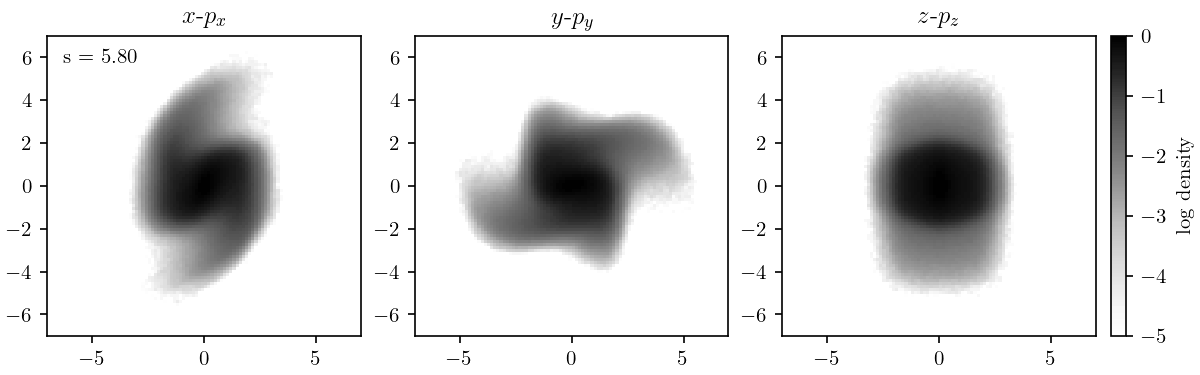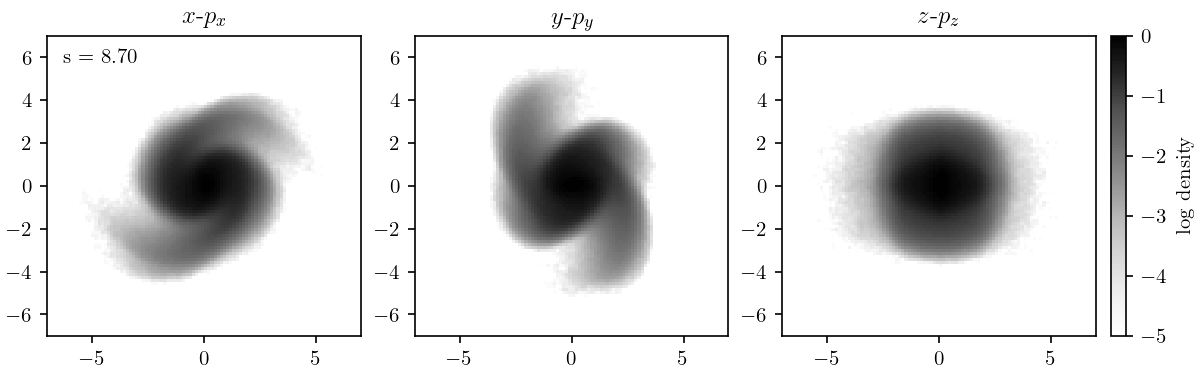
In the previous post I showed the first high-dynamic-range PIC simulation benchmark of the beam dynamics in the SNS Beam Test Facility (BTF). The most striking observation from these studies is that the two-dimensional phase space projections develop low-density spiral arms. Spiral patterns are generic features of nonlinear dynamics: in a linear system, all particles rotate by the same angle in phase space, but in nonlinear systems, the rotation angle depends on the particle amplitude.

It’s interesting to trace the development of these spirals within the accelerator. The following figures show the two-dimensional distributions on the \(x\)-\(p_x\), \(y\)-\(p_y\), and \(x\)-\(y\) planes. The coordinates are normalized such that the covariance matrix \(\mathbf{\Sigma} = \langle \mathbf{x} \mathbf{x}^T \rangle = \mathbf{I}\), where \(\mathbf{I}\) is the identity matrix and \(\mathbf{x} = (x, p_x, y, p_y)\). In these coordinates, linear forces leave the distribution invariant; all changes are due to nonlinear forces.

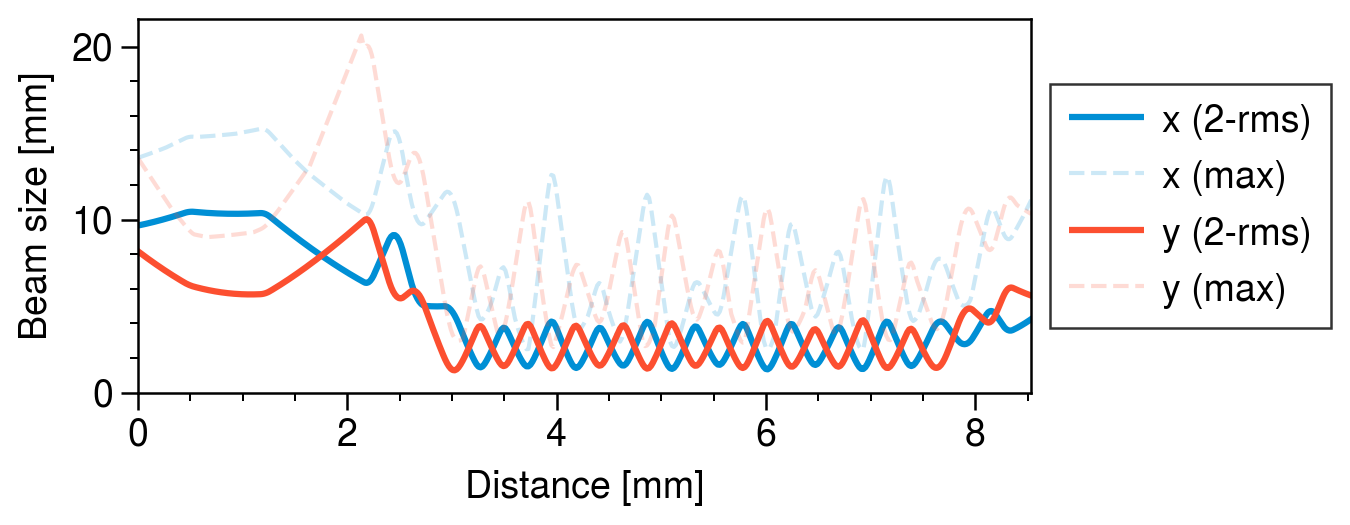
The initially slow rotations occur before the FODO line, while the fast rotations occur in the FODO line, where the beam size oscillates rapidly.