Reconstructing the 4D phase space density of a high-power proton beam from 1D measurements in the SNS ring
In the previous post, I discussed numerical experiments to test an approximate high-dimensional maximum-entropy phase space tomography algorithm by modifying the Generative Phase Space Reconstruction (GPSR) approach. I recently applied this approach to reconstruct the 4D phase space distribution of a high-power proton beam in the SNS ring.
Eigenpainting
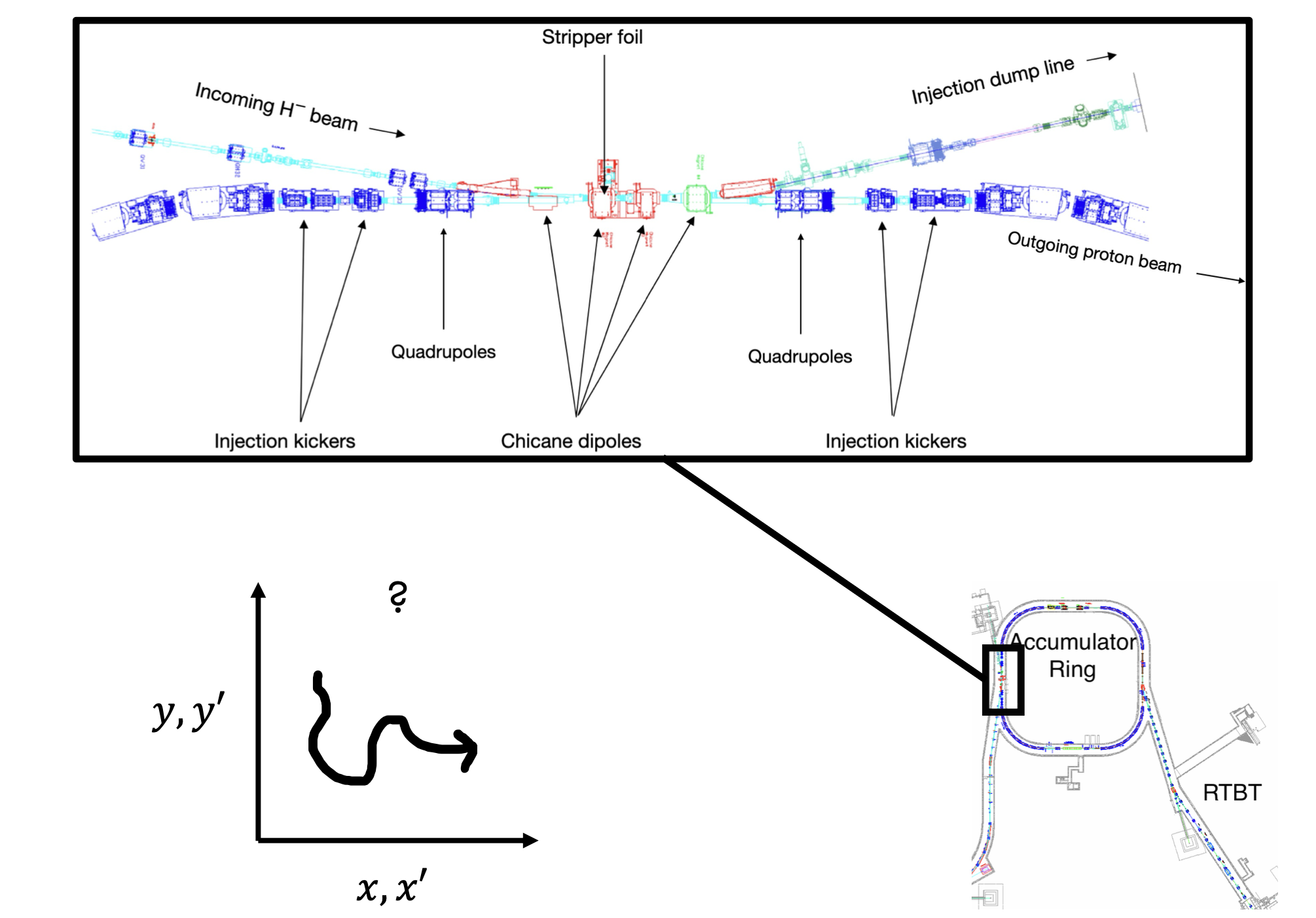
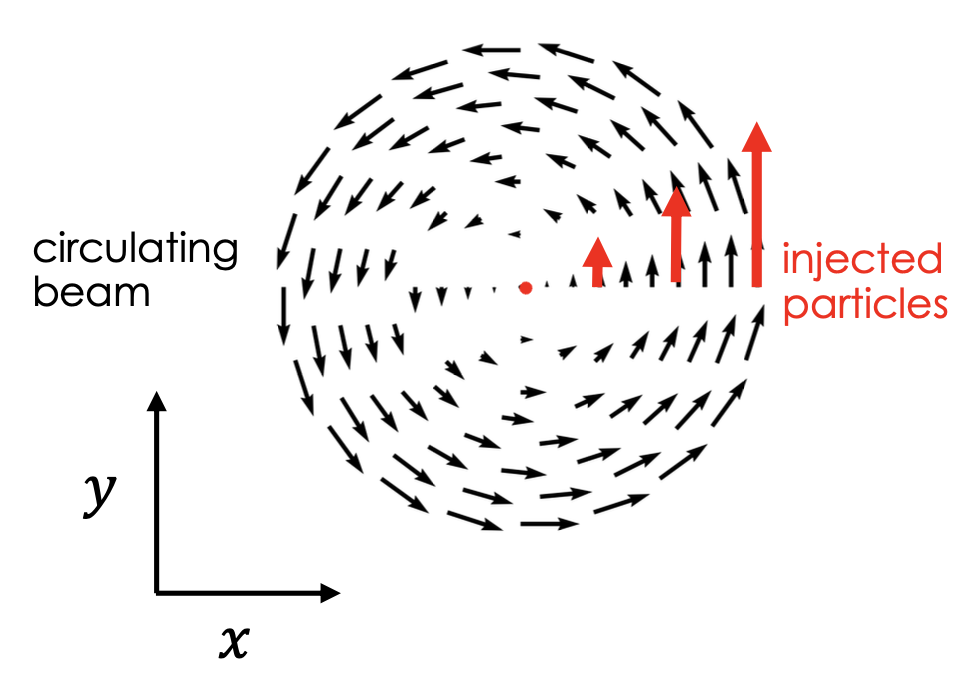
The SNS accelerates H- ions to 1 GeV, strips the electrons, and injects the remaining protons into a ring. After 1000 injected turns, the accumulated pulse contains over \(10^{14}\) protons—over 1 MW of beam power when operating at the full 60 Hz repetition rate. Some more info on the injection scheme is here. Injecting all particles in a tiny region would lead to an enormous charge pileup and emittance growth. Thus, we slowly move the circulating beam away from the injected beam during injection to fill the phase space more uniformly.
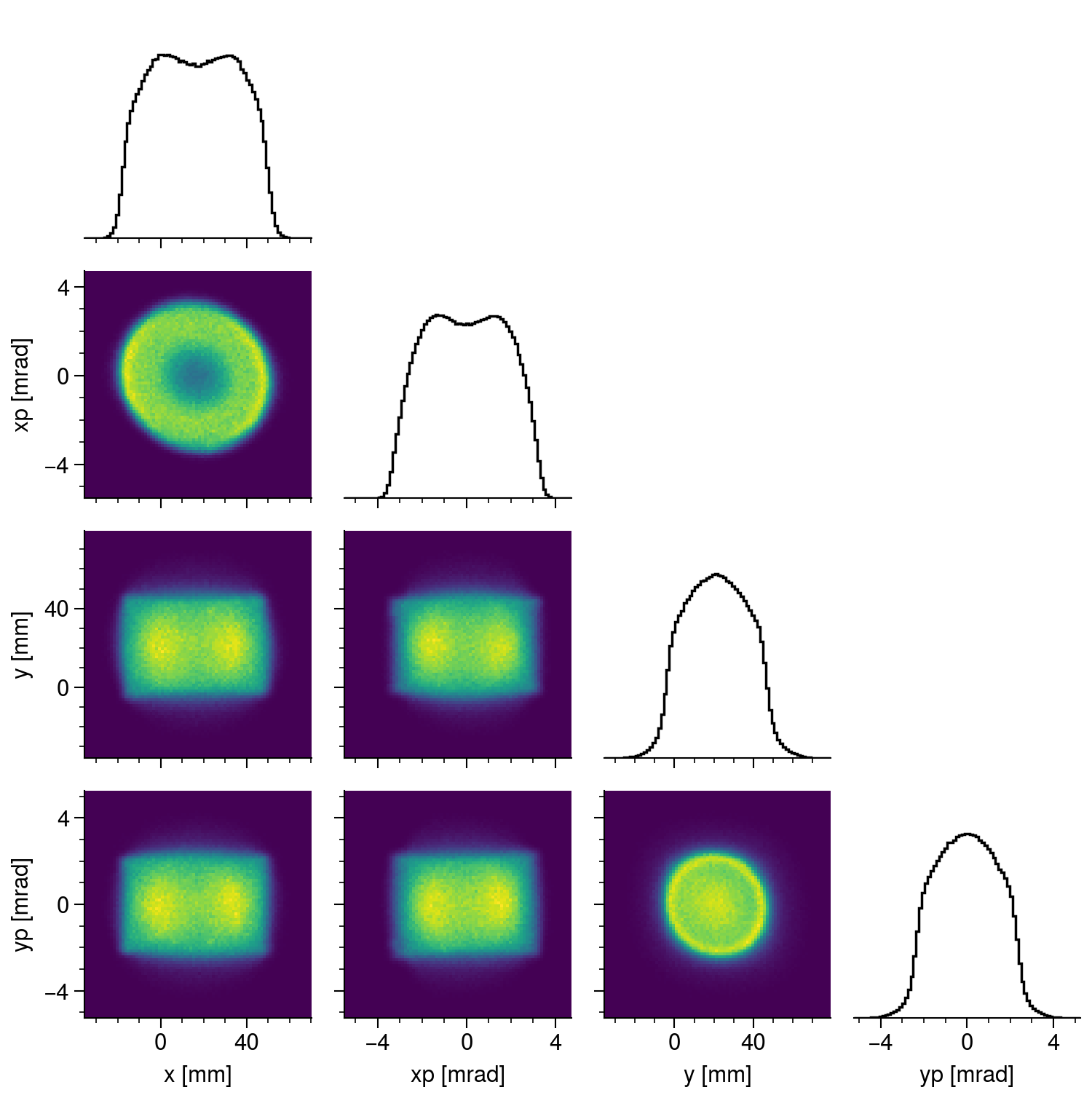
The SNS starts with a large offset between the injected and circulating beams. At one position in the accelerator, the turn-by-turn particle coordinates jump around an ellipse in 2D phase space (\(x\)-\(x'\), \(y\)-\(y'\)); thus, the 2D phase space distributions \(\rho(x, x')\) and \(\rho(y, y')\) begin as donuts. Nonlinear and collective effects cause filamentation, filling in the donuts. We end up with a somewhat uniform density rectangular distribution in the \(x\)-\(y\) plane. Figure 1 plots a typical simulated beam using this “production” setup.
When we move the circulating beam away from the injected beam, we effectively change the phase space coordinates of the injected particles. In the scheme above, we use time-varying dipole magnets to adjust the position \(x\) (or \(y\)). We could also use the same magnets to change the momentum \(x'\) (or \(y'\)) by introducing an angle between the injected and circulating beams. By varying the dipole magnet currents as a function of time, we move the injection point through the \(x\)-\(x'\) phase space. Phase space painting thus seems like an appropriate name.
We could extend phase space painting to four phase space dimensions by introducing correlations between the horizontal and vertical dipole strengths. We then trace a line through the 4D phase space \(x\)-\(x'\)-\(y\)-\(y'\): \(\mathbf{x}(t)\), where \(t\) represents either the time or the turn number. 4D phase space painting might enable more precise control of the beam distribution, but no one has tried it.
Some time ago, Slava Danilov (ORNL) proposed a 4D phase space painting technique, which we now call eigenpainting. The idea is to create coupling in the ring using solenoid or skew quadrupole magnets, then to inject particles along an eigenvector of the \(4 \times 4\) ring transfer matrix \(\mathbf{M}\).
\[ \mathbf{M} \mathbf{v}_k = e^{-2 \pi \nu_k} \mathbf{v}_k, \]
where \(\mathbf{v}_k\) are the eigenvectors, \(\nu_k\) are the tunes, and \(k = 1, 2\). In general, particle motion is a linear combination of the eigenvectors:
\[ \mathbf{x} = \Re \left\{ \sum_k \sqrt{2 J_k} \mathbf{v}_k e^{\mathbf{i \psi_k}} \right\}, \]
where \(J_k\) are amplitudes, \(\psi_k\) are phases, and \(\Re\) selects the non-imaginary component. In eigenpainting, we inject particles into the ring with \(J_1 \gg J_2\). If we continuously injected particles in this way at a fixed amplitude, the particles would eventually uniformly populate an invariant closed surface in the 4D phase space. If we scaled the injection amplitude, we would fill another surface enclosing the first. It would be like adding a layer of paint to “The Rock” at the University of Michigan.
Each eigenvector traces an ellipse when projected onto any 2D subspace, so we could generate a uniform charge density within an ellipse in the \(x\)-\(y\) plane by scaling the injection amplitude as the square root of time.
\[ \mathbf{x}(t) = \Re \left\{ \sqrt{2 J_k} \mathbf{v}_k e^{\mathbf{i \psi_k}} \right\} \sqrt{t}. \]
We would also generate a vortex velocity field, illustrated in Figure 4. The distribution would live on a 2D surface in the 4D phase space, and the 4D phase space volume, or emittance, would be zero.
Things become much more complicated when particles interact through the Coloumb force. These so-called space charge interactions generally invalidate the assumption of linear dynamics. But, surprisingly, eigenpainting works even with space charge. The distribution described above is an equilibrium solution to the Vlasov-Poisson equations, which describe the self-consistent evolution of a phase space distribution under applied focusing forces and intense space charge fields. Equilibrium distributions maintain their functional form over time, even under intense space charge forces. This is not at all trivial. Our distribution, which we call the Danilov distribution, generates space charge forces that are linear in the \(x\) and \(y\) displacements, and the linearity of the space charge force is maintined for all time. It means we can still describe the particle motion using a transfer matrix as long as this transfer matrix includes the self-consistent space charge forces from the beam. Thus, eigenpainting works at any beam intensity.
A Danilov-like distribution could have significant benefits for accelerator performance. Linear space charge forces result in the same tune shift (change in oscillation frequency) for every beam particle. Space-charge-driven tune spread is a significant intensity limitation in high-intensity rings. Paricle-core resonances driven by nonlinear space charge may also be reduced. Several authors have additionally shown that angular momentum can blur particle-core resonances and enhance beam stability. Thus, perhaps eigenpainting could bypass space charge limitations and produce higher-intensity hadron beams.
In addition to reduced space charge effects, the beam’s angular momentum could benefit high-energy hadron colliders. High-energy hadron colliders, such as the LHC, begin with an H- linac and injection into a low-energy ring. Generating a beam with low 4D emittance in these early stages makes it possible to flatten the beam at later stages to boost the collision luminosity. The 4D emittance is typically lower-bounded by space charge effects at low energy, but with eigenpainting, one could generate a small 4D emittance beam of arbitrary intensity.
SNS experiments
We’ve been working on testing the eigenpainting method in the SNS ring. These experiments have been very frustrating, typically taking 6-8 hours to set up the ring and leaving little time for experiments. And we only get a maximum of one experiment per month. However, we do have some initial results that look promising. I won’t describe the details of the experiment here. Essentially, we set up the ring and programmed the injection kickers to perform the painting method as best we could under various constraints that don’t show up in simulations. Then we injected the beam.
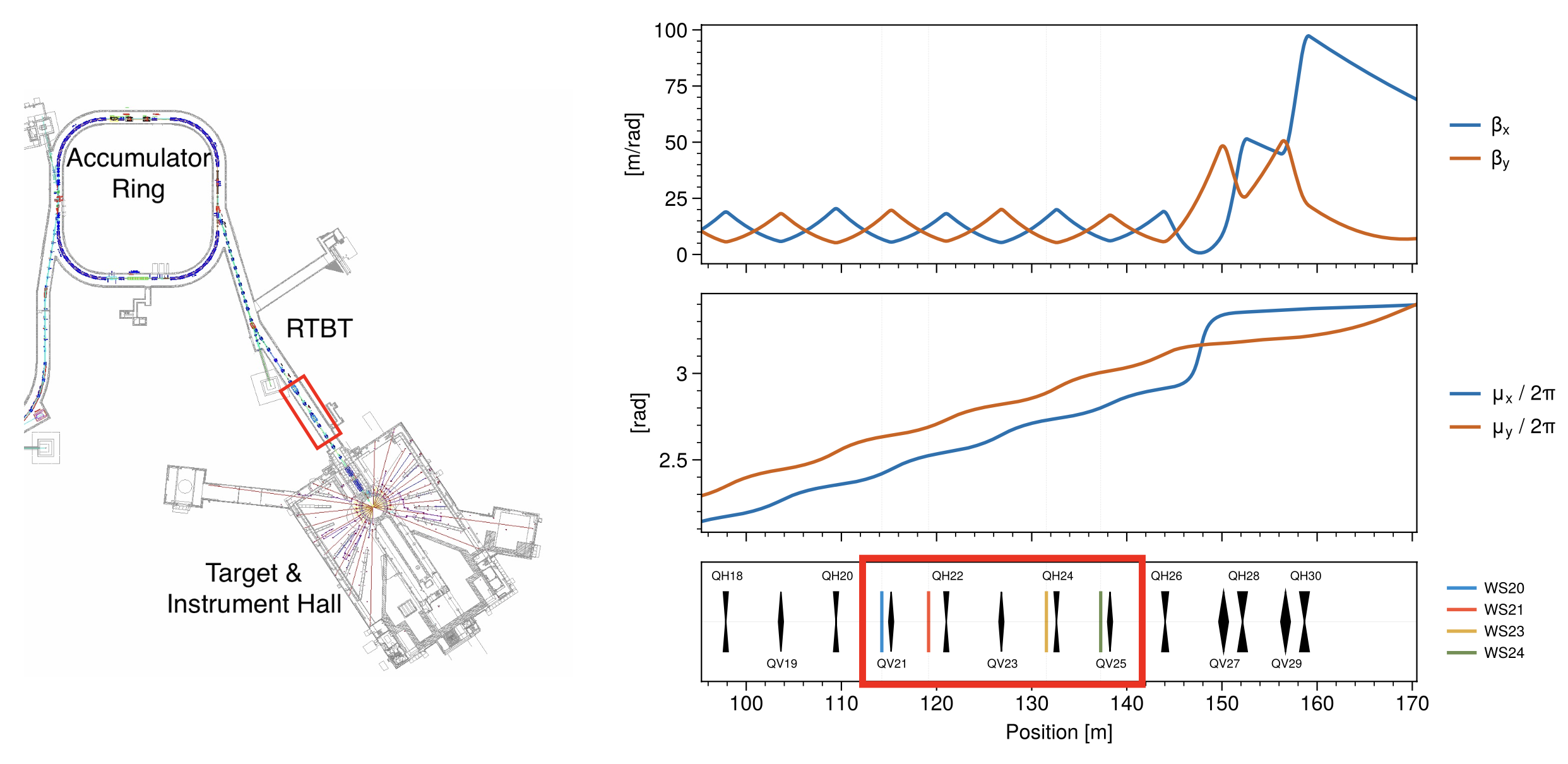
I’ve been focusing on how to measure the beam during injection. We’re looking to measure strong linear correlations between planes, indicating a small four-dimensional emittance, and to measure the uniformity of the charge density in the transverse plane. Our diagnostics are limited. We can’t measure the beam in the ring, but we can extract the beam on a specific turn and send it to the target. The Ring-Target Beam Transport (RTBT) line, shown in Figure 6, contains several wirescanners. Each wirescanner has a horizontal, diagonal, and vertical wire, generating vertical, horizontal, and diagonal profiles. The wirescanners run in parallel, so a single measurement generates twelve profiles. Since the wirescanners are at different locations along the beamline, each profile corresponds to a different projection axis in the 4D phase space at some point upstream of the wirescanners.
In this paper, I found that these twelve profiles do not determine the 4D covariance matrix. There are constraints on the beam size and minimal control over the phase advances, but we found a slightly better set of optics for the 4D reconstruction. Although one set of measurements can generate a noisy estimate of the 4D covariance matrix, it’s better to take two or three. Unfortunately, this takes time: each measurement takes nearly five minutes! The wirescanners actually measure many different beam pulses as they slowly step through the beam and back to their starting points. If we collect three sets of optics, we’re looking at fifteen minutes per measurement. That severely limits the number of measurements we can take in our limited beam study periods. In our latest experiment, after finally getting the machine set up properly, we were able to take three good sets of wire scans, generating 36 one-dimensional profiles.
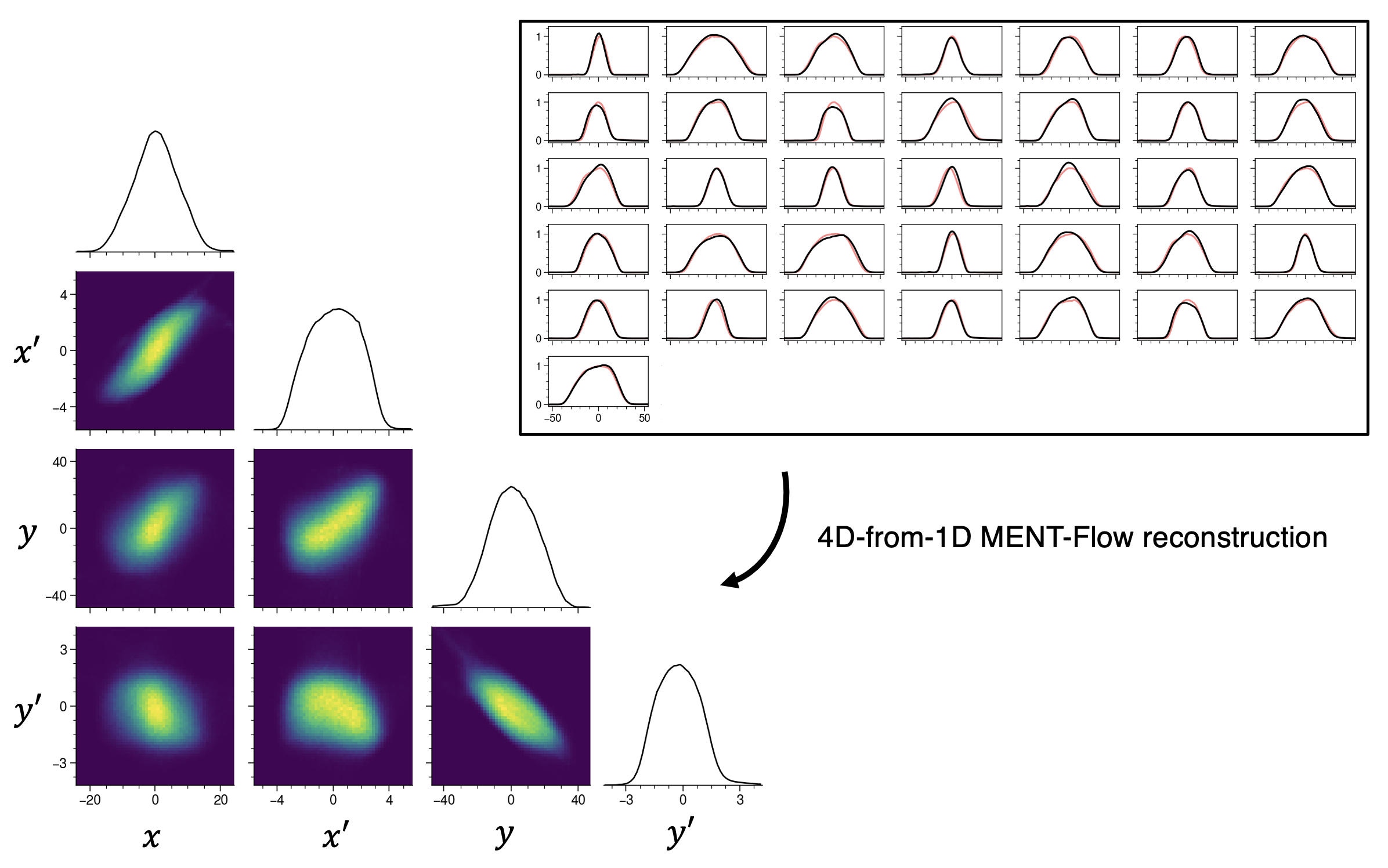
Although we aimed to measure the emittance, I realized we could apply MENT-Flow to the same data to estimate the 4D phase space density. During my PhD, I tried to do this using the image of the beam on the target, but the image ended up being too noisy, so I gave up. The wirescanner measurements are more reliable, but it’s unclear if the 1D projections in the RTBT provide enough information to constrain the 4D distribution. That’s the perfect time to use entropy maximization! (Actually, MaxEnt is always the right choice, but it’s most important when data is scarce.)
We assumed the accelerator lattice could be described by linear focusing elements and, hence, linear transfer matrices connecting the reconstruction to the diagnostics, so it was straightforward to implement a differentiable accelerator model. I then ran MENT-Flow using a Gaussian prior based on the measured covariance matrix. Here’s the reconstruction result:
The fits aren’t perfect. After extensive testing with known ground-truth distributions, I’m confident that MENT-Flow should be able to fit the distribution to this measurement set and that the result should be close to the true distribution. However, there could be errors in our beam dynamics model or measurements. It’s unclear how to determine the problem.
The fits aren’t perfect, but they’re still pretty good! There are only a few bad apples. The overall good fit, combined with the entropic regularization, makes me confident that the primary features in the distribution are real. We observed two things. First, there are clear cross-plane dependencies in the reconstructed distribution. The correlations are not nearly as strong as we intended, but their presence tells us we’re moving in the right direction. Second, the beam density is not purely Gaussian; the data have pulled the reconstruction toward something more uniform. A uniform beam density is also a goal of the eigenpainting method. Although the beam density is not as uniform as we’d like it to be, it’s again encouraging that we’re moving in the right direction.
I’m using simulations to understand how space charge and other effects degrade the beam quality during injection, blurring these correlations by the time we measure the beam. From my studies thus far, I think it’s very likely that strong space charge effects—amplified by the low 0.8 GeV beam energy and small beam size—significantly impacted the beam dynamics. 4D phase space tomography gives us a more powerful comparison to simulations and visually striking communication of our results.