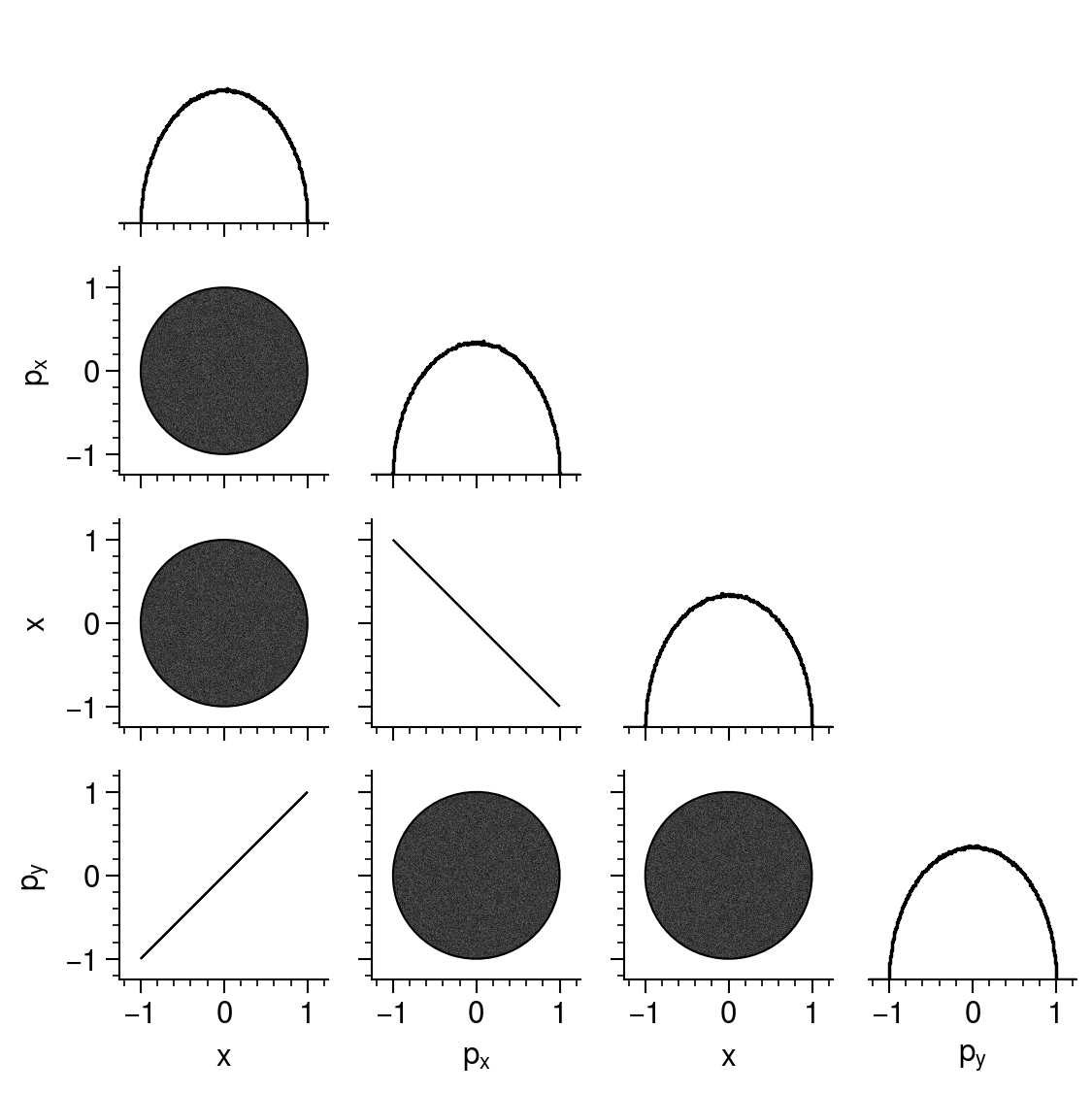
umin = np.min(sizes)
umax = np.max(sizes)
umax_pad = 1.25 * umax
fig, axs = pplt.subplots(
nrows=2,
ncols=2,
figsize=(7, 2.5),
spany=False,
aligny=True,
sharey=False,
sharex=False,
hspace=0.2,
height_ratios=[5.0, 1.0],
width_ratios=[2.75, 1.0],
)
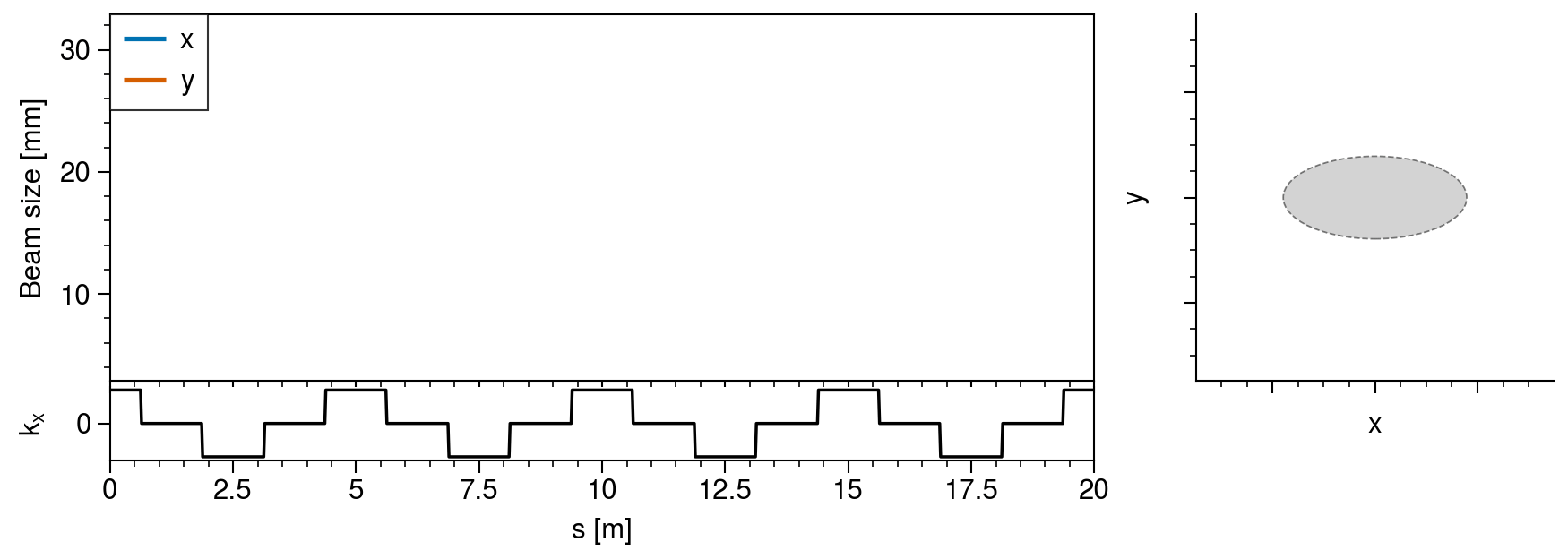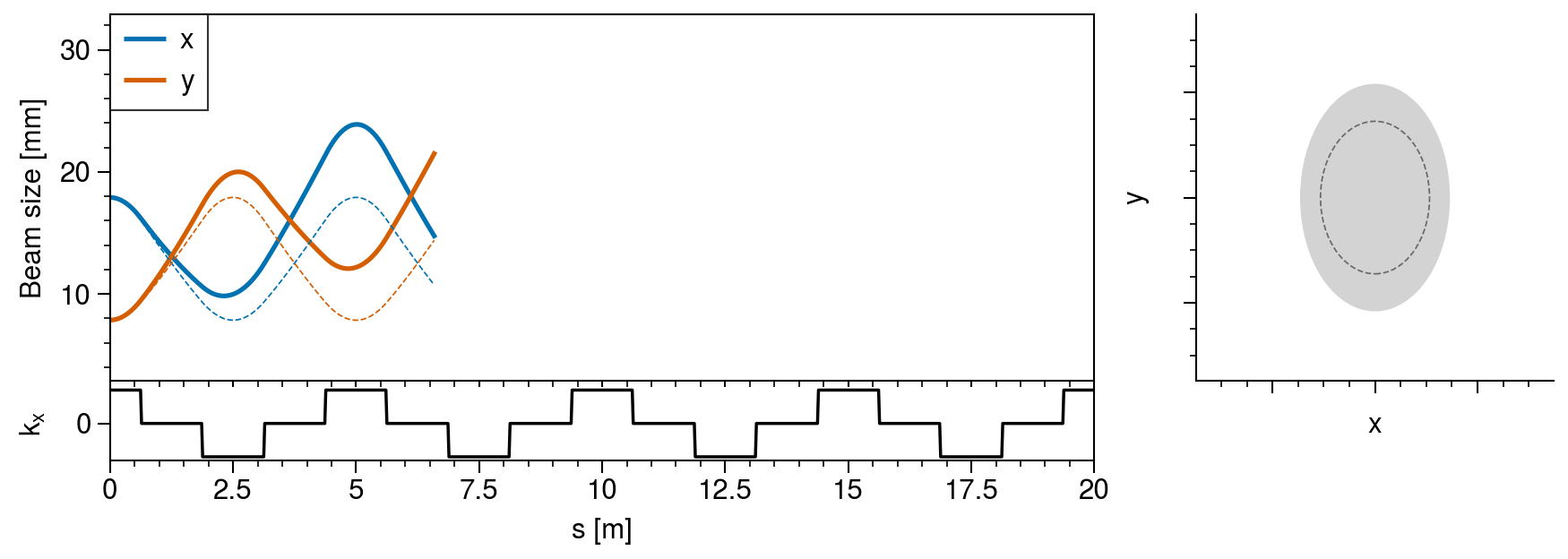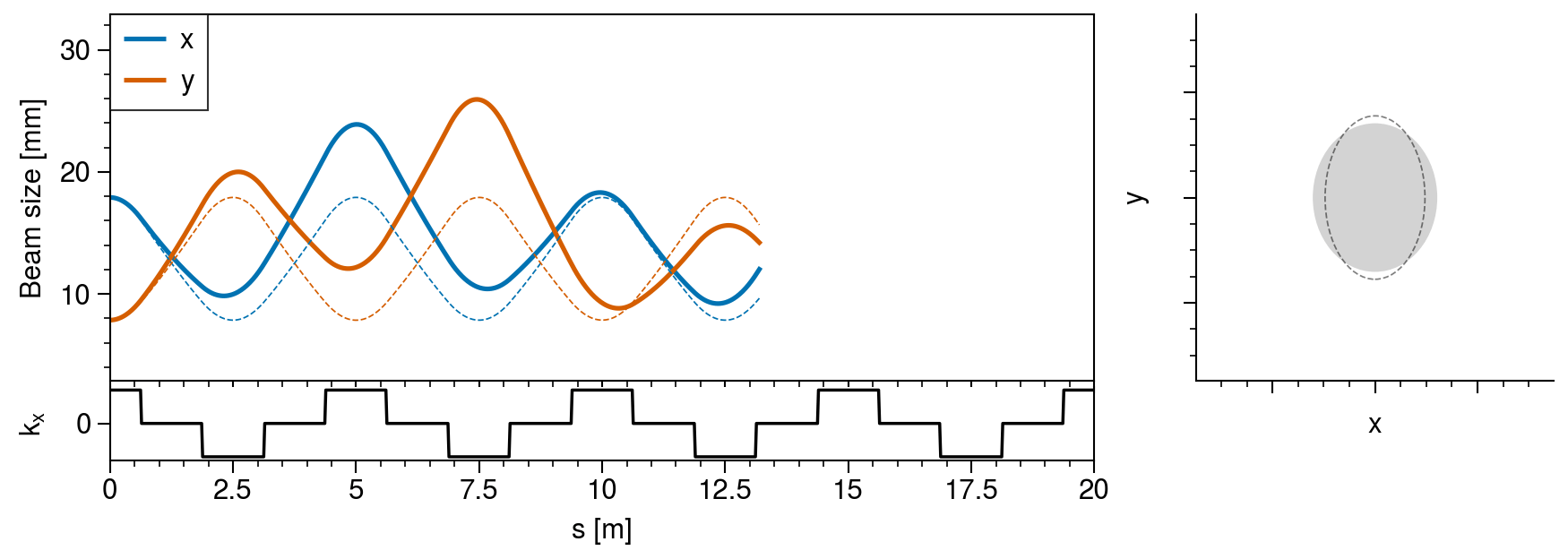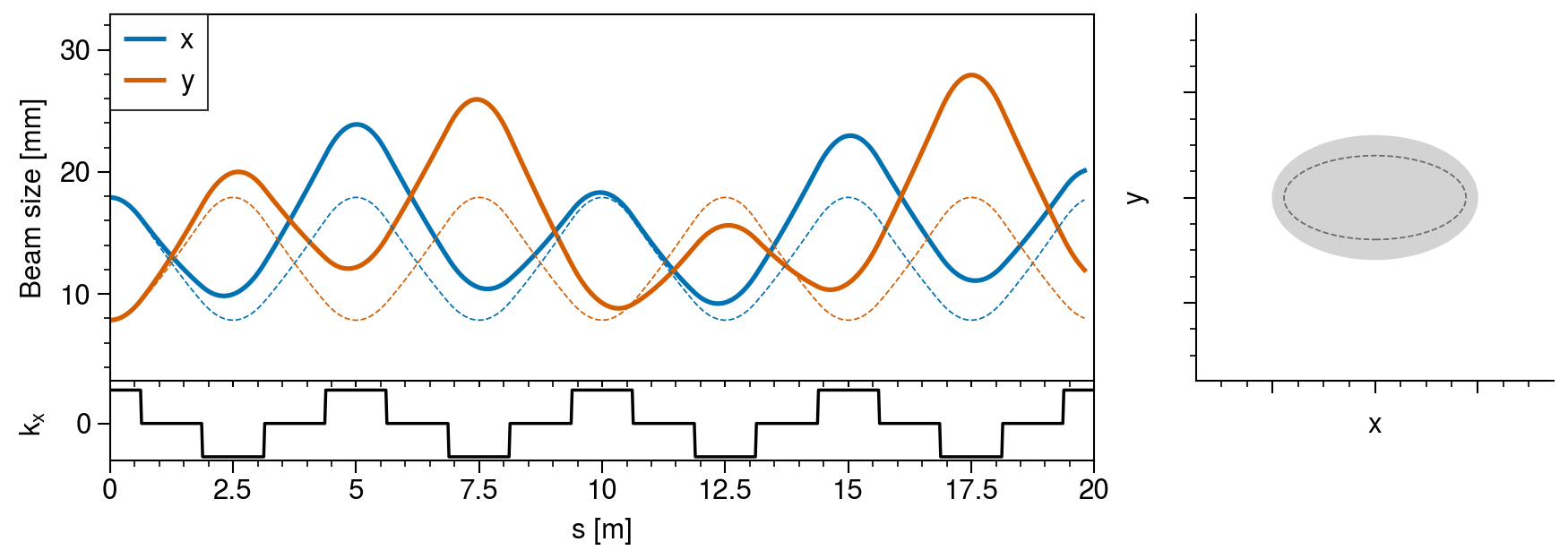
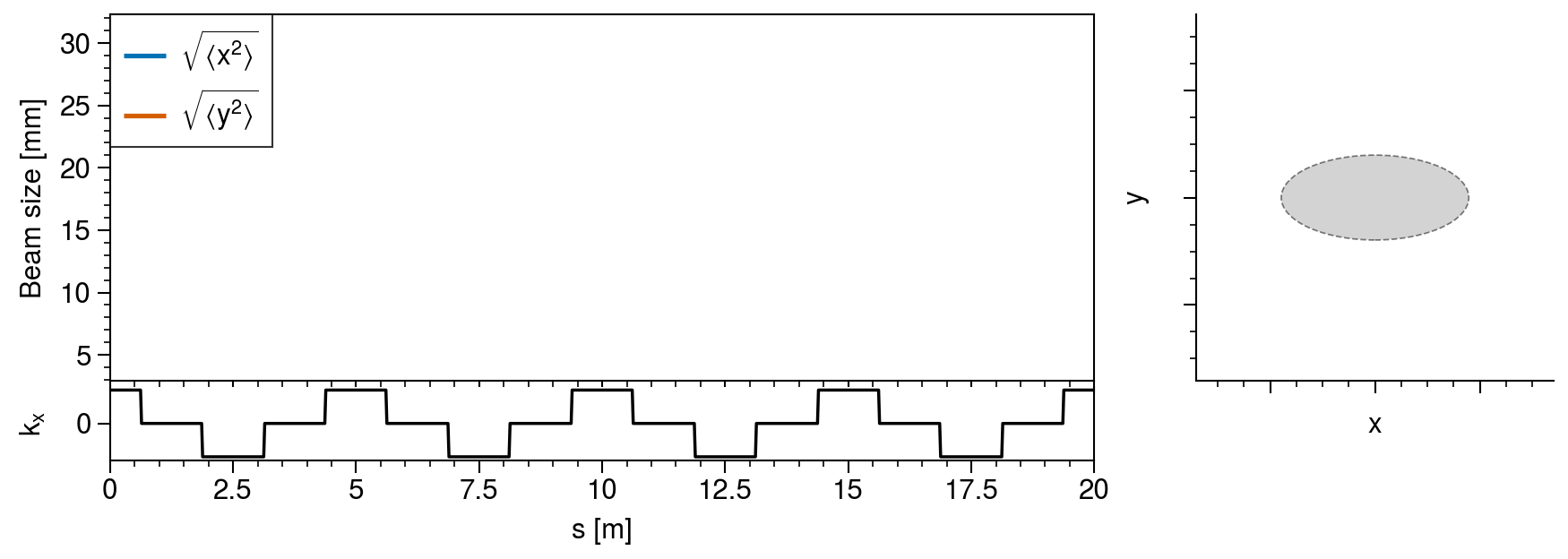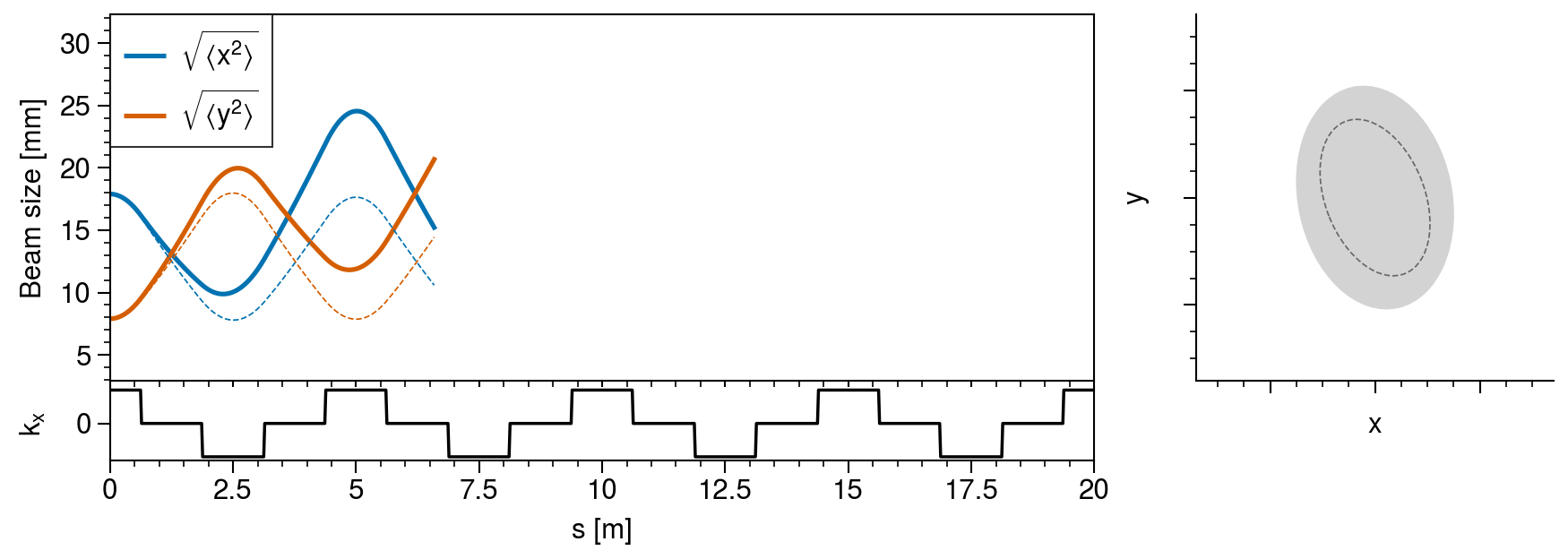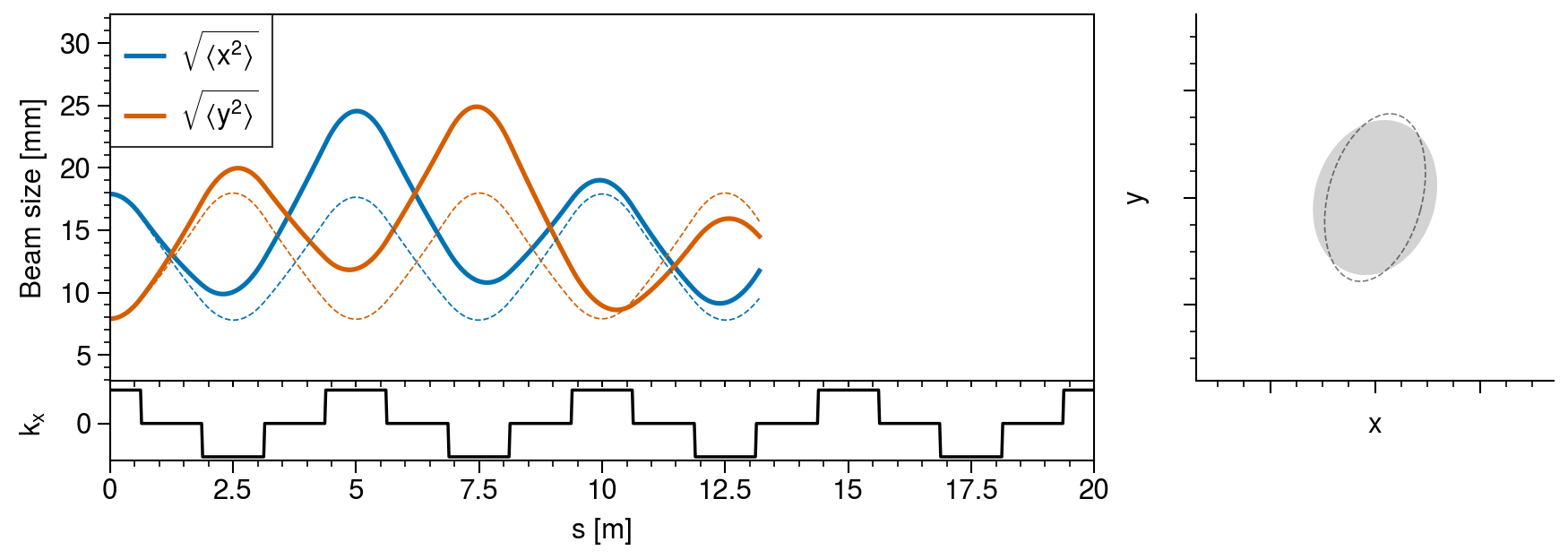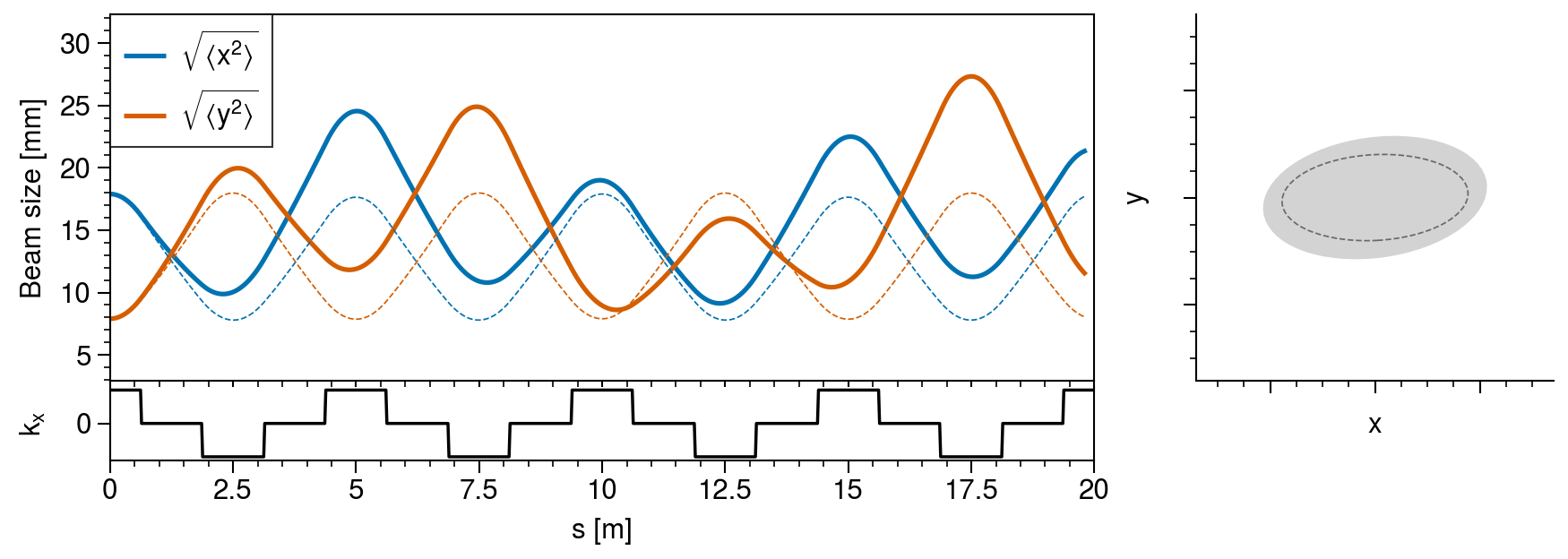
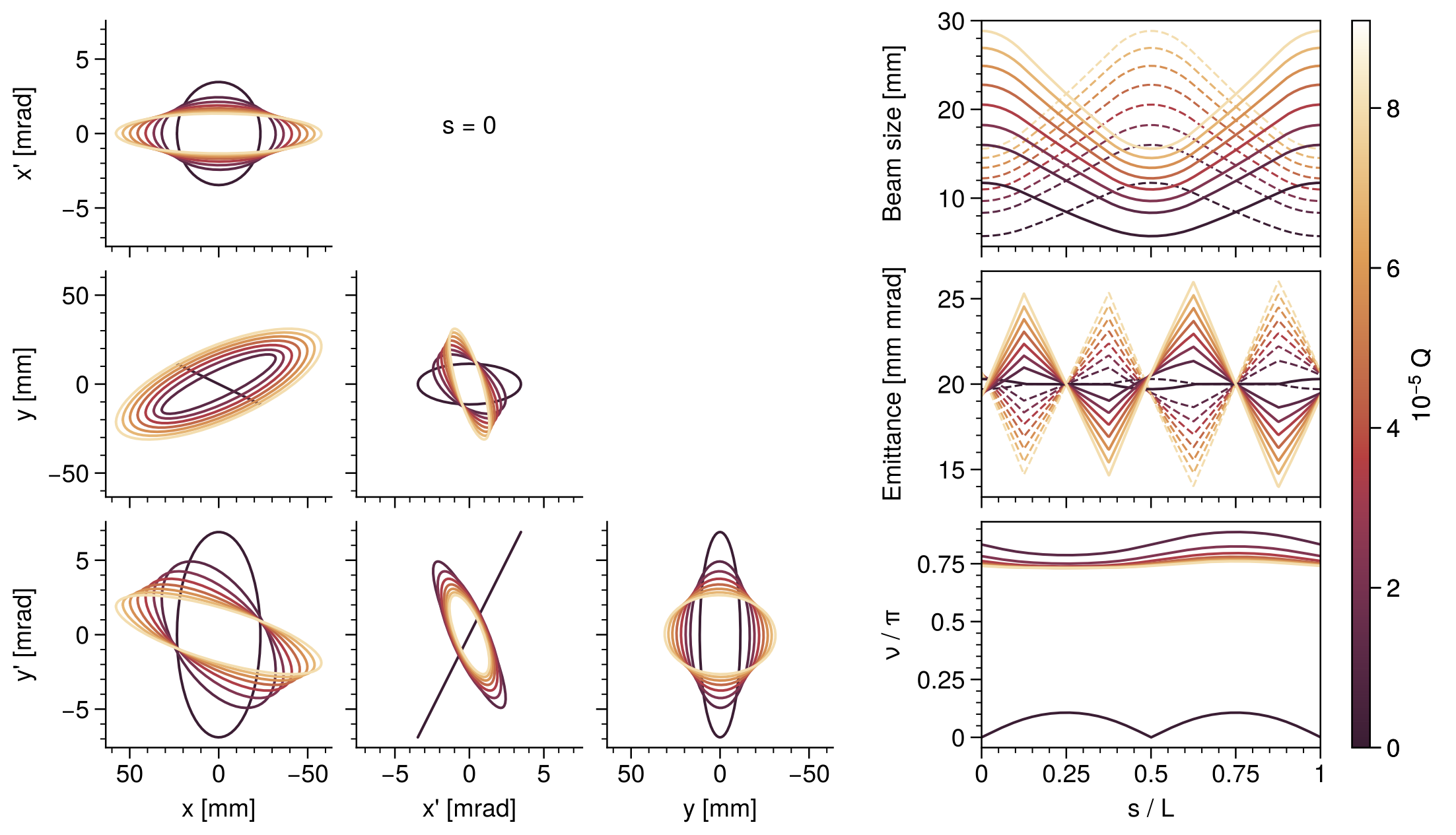
axs[0, 0].format(xlabel="", ylabel="Beam size [mm]", ylim=(umin - 5, umax + 5))
axs[1, 0].format(xlabel="s [m]", ylabel=r"$k_x$", yticks=[0], ylim=(-0.6116, 0.6116))
axs[:, 0].format(xlim=positions[[0, -1]])
axs[1, 0].spines["top"].set_visible(False)
axs[0, 1].format(
xticklabels=[],
yticklabels=[],
xlabel="x",
ylabel="y",
xlim=(-umax_pad, umax_pad),
ylim=(-umax_pad, umax_pad),
)
axs[0, 1].format(xspineloc="bottom", yspineloc="left")
axs[1, 1].axis("off")
axs[0, 0].format(xticklabels=[])
axs[0, 0].legend(
handles=[Line2D([0], [0], color=colors[0]), Line2D([0], [0], color=colors[1])],
labels=[r'$\sqrt{\langle{x^2}\rangle}$', r'$\sqrt{\langle{y^2}\rangle}$'],
ncols=1,
loc="upper left",
fontsize="small",
handlelength=1.5,
)
axs[1, 0].plot(positions, [fodo(s) for s in positions], color="k", lw=1)
plt.close()
line1, = axs[0, 0].plot([], [])
line2, = axs[0, 0].plot([], [])
axs[0, 0].format(cycle='colorblind')
line3, = axs[0, 0].plot([], [], ls='--', lw=0.5)
line4, = axs[0, 0].plot([], [], ls='--', lw=0.5)
def update(i):
i *= stride
line1.set_data(positions[:i], sizes[:i, 0])
line2.set_data(positions[:i], sizes[:i, 1])
line3.set_data(positions[:i], sizes0[:i, 0])
line4.set_data(positions[:i], sizes0[:i, 1])
for patch in axs[0, 1].patches:
patch.set_visible(False)
axs[0, 1].add_patch(
Ellipse(
(0, 0), 2.0 * radii[i, 0], 2.0 * radii[i, 1], angles[i],
fc='lightgrey', lw=0.75, ec='None'
)
)
axs[0, 1].add_patch(
Ellipse(
(0, 0), 2.0 * radii0[i, 0], 2.0 * radii0[i, 1], angles0[i],
fill=False, ls='--', color='k', lw=0.5, alpha=0.5,
)
)
anim = animation.FuncAnimation(
fig, update, frames=len(positions[::stride]), interval=(1000.0 / 14.0)
)
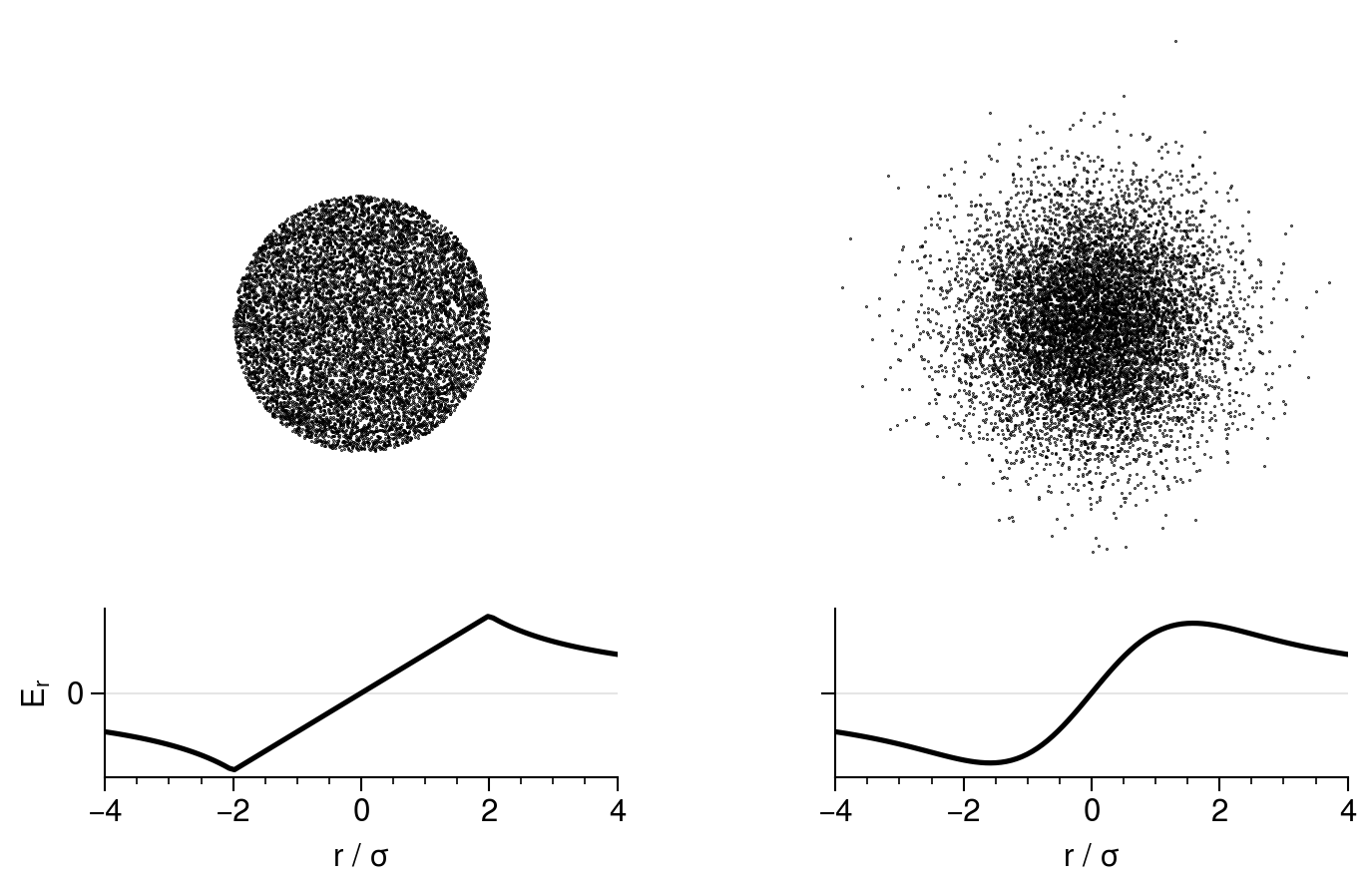
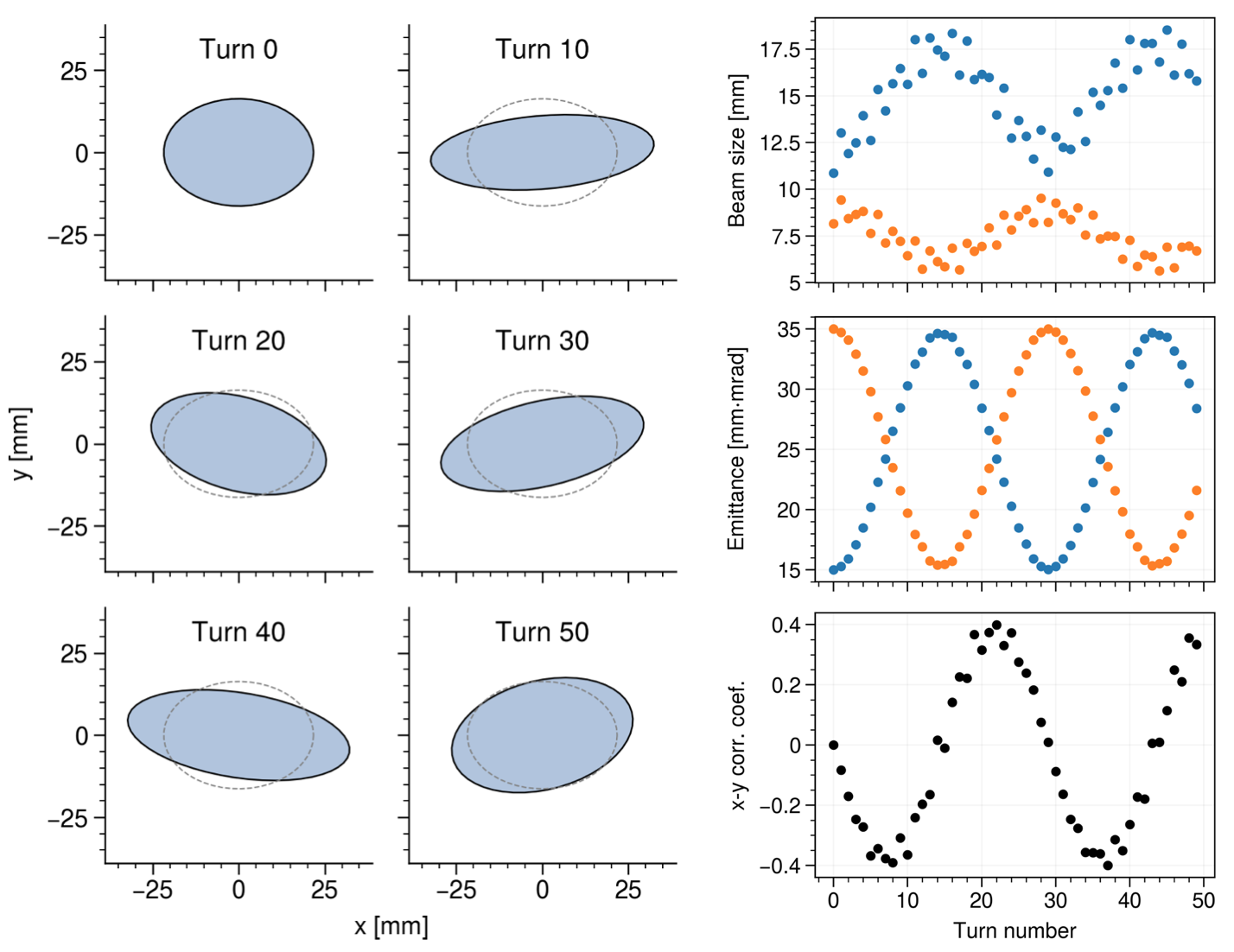
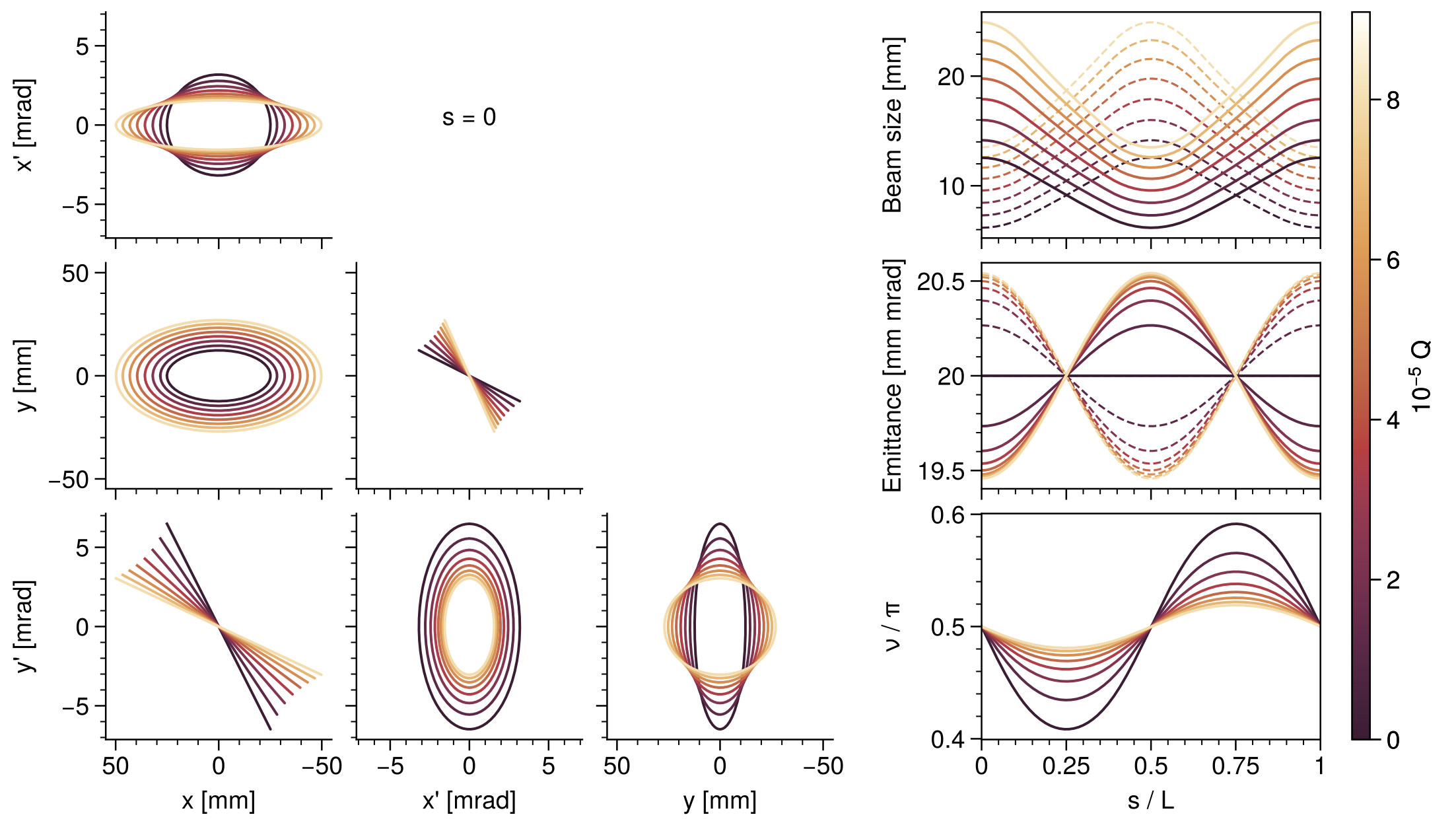
![Fig. 2. Emittance growth in an intense beam propagating in a linear accelerator. The emittances \varepsilon_{x,y} correspond to the areas in the projected phase spaces x-p_x and y-p_y (Source: [2].)](fig7.png)
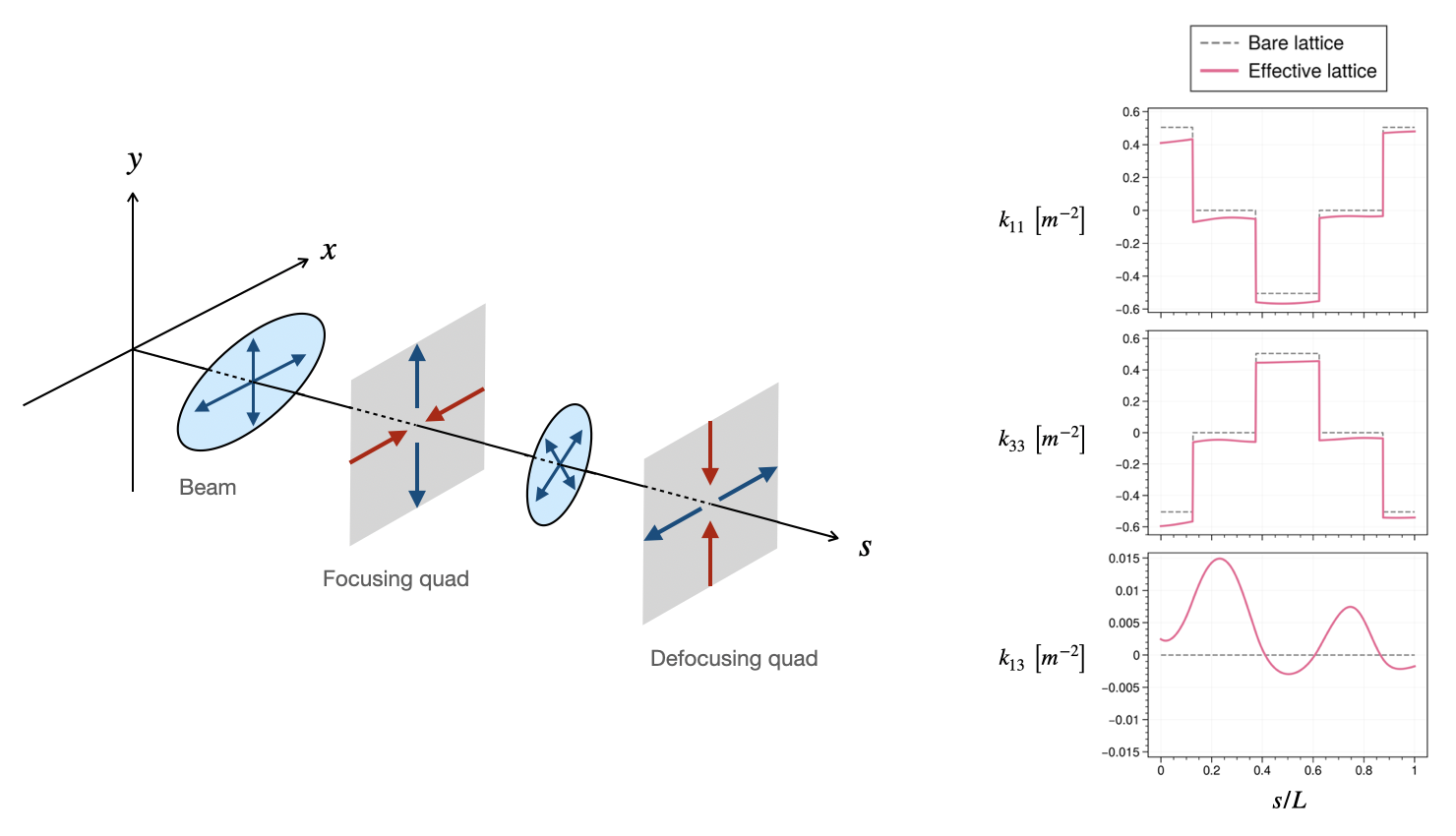
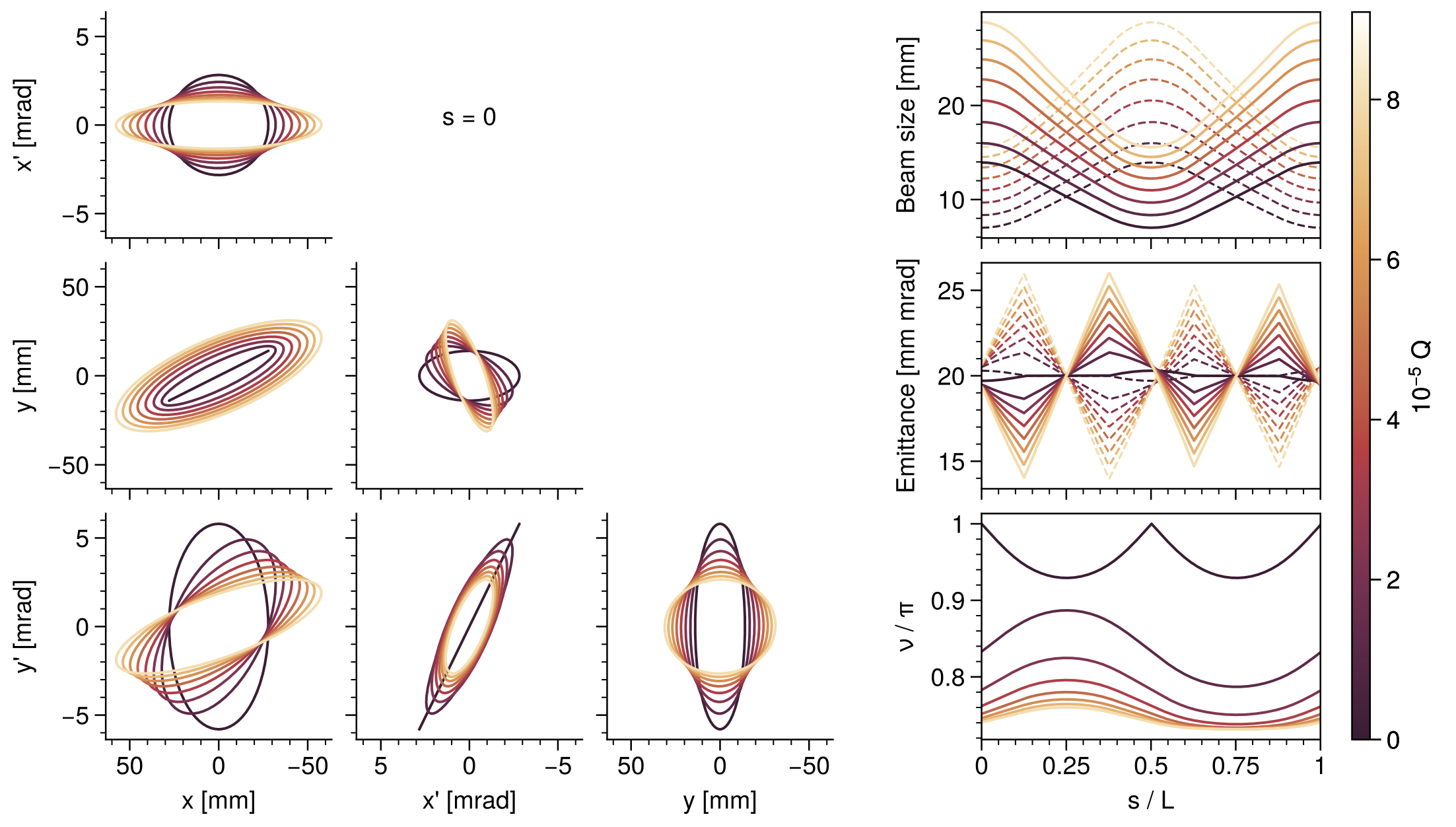
![Fig. 3. Simulated tune spread in the SNS ring. (Source: [3].)](fig6.png)